| ↑ Home |
Separation between formatted printing to stdout and string
buffers shall be resolved. Formatted printing to stdout
shall be removed in favor of string buffers.
Moss gets a function and syntax for formatted printing. I will compare it with equivalents from C.
C: printf("(%li,%li)",x,y)
Moss: print("({},{})"%[x,y])
C: snprintf(s,N,"(%li,%li)",x,y)
Moss: s = "({},{})" % [x,y]
The template syntax will be similar to format
from Python but may differ more or less.
# Here is an example of proper usage:
a = list(0..10).map(|x| [x,x^2])
buffer=[]
for t in a
buffer.push("({},{})"%t)
end
s = buffer.join("\n")
print(s)
# More briefly:
/*1*/ a = list(0..10).map(|x| [x,x^2])
/*2*/ s = a.map(|t| "({},{})"%t).join("\n")
/*3*/ print(s)
We see a practical pattern: a strict separation between actual information structure (1), formatting (2) and stdout (3).
Note: to have advanced output, libraries should be provided that return tables as HTML5, LaTeX2e and plots as PNG, SVG as automatically as possible. Whole documents or books (libraries?) could be generated automatically from data. But one must say to this, that HTML5 is more easy to use than LaTeX2e.
As sets are a special case of maps (dictionaries) and set operations do not interfere with map operations, them can be joined. Maps with values absent can be considered as sets:
{1, 2} == {1: null, 2: null}
Multisets cannot be included as well, because
they introduce problems. For example, '==' behaves
differently if there are keys with m[key]==0.
But it is clear that maps may be used as internal data
structures of multisets. An alternative is, to simpliy monkey patch
the neccessary operations into Map
(Map is the data type of maps).
A syntactical sugar for assignments to function applications is added to the language.
1. a.m()=y is equivalent to a.set_m(y)
2. a.m(x1,...,xn)=y is equivalent to a.set_m(x1,...,xn,y)
3. a.m(x) = y1,y2 the same as a.m(x)=[y1,y2]
and therefore equivalent to a.set_m(x,[y1,y2])
4. a.m1(),a.m2() = t is not possilbe (t=[y1,y2])
5. a[i]()=y is not possible
The point in (4) is that the language should be minimalistic and (4) would blow it up. It is definitely much harder to implement than (1,2,3) which required less than 40 lines of code.
There is a problem with standard printing of floating point numbers. For example, one can get
> list(0..1:0.2) [0.0, 0.2, 0.4, 0.6000000000000001, 0.8, 1.0]
So we can have output of the form 000000000...some digit
and (under other circuumstances) 999999999...some digit.
This is because of printf("%.16g\n",x).
In most cases one has engineering tasks and does not suffer
from slightly lower precision. So I think I will change that
to %.14g to make output more stable. One can always get full
precision by "{g16}"%[x] or even "{g17}"%[x].
(#include <float.h>: DBL_DECIMAL_DIG==17)
It is clear for me now, that the Moss interpreter must be rewritten in Rust. I have to struggle with segmentation faults too often. The security goals are:
Security (1). Maybe it is possible to achieve a memory safe implementation.
Security (2). Access to files will be realized by a mandatory access control system. In that system the main program obtains a right to access files in some path. This right is given explicitly to the subprograms that do the task. The difference to the flat model is, that in the flat model a third party library routine can do anything, once the main program got the right.
Security (3). What makes the most headache is a general call of shell commands. Any call of an external program (e.g. in a scripting language) can undermine the access control system. Thus such a call is ill behaved and shall only be possible in the unsafe mode. Ideally, the unsafe mode is made forbidden outside of a sandbox environment.
Update (2018-03-22). The interpreter kernel is ported to Rust, it's construction was successful and is is almost complete now. There were some pitfalls, interesting ones, but it was possible to take them into account. The most interesting pitfalls are:
env has to be given
to every Rust function that needs to call a Moss function or needs to
have access to the RTE (runtime environment). This is
much less obfuscated than handling global variables.
gtab
(table of global variables) of its module. And the module has a
pointer to this function. Therefore we have a cyclic data structure
that turns out to be a memory leak.
One could have used a weak pointer, but that would have made things
complicated. The best solution was to add a destructor at the
destruction of the interpreter that clears the gtabs.
A small difficulty remains: If a module shall be unloaded properly
sooner than at the ending of the main program,
this destructor must be called explicitly.
Drop, Eq,
Hash cannot take env,
nor can they return error information. A solution I have found for
env is to store a RTE pointer in a table object
(the implementation is inside of TableExtra), and to
store a stack of alternative calling environments in the RTE.
This is my worst problem so far, but it only affects custom Moss
destructors and hashables.
Security goal (1) is achieved, the interpreter is memory safe, provided Rust is sound, the Rust compiler produces safe code and each used FFI (foreign function interface) is safe. It is also possible to make it almost completely logically safe in terms of overflow checks (there is a compiler option for that). There are some remaining overflows from integer casts that should be audited. Inline functions can be used to abstract this, making the overflow checks optional.
Security goals (2) and (3), running untrusted code by a capability-based security model, are much harder to achieve, because this security model is deeply connected to privateness and immutability of data. For file access, a model with sandbox directories seems to be, albeit less fine grainded, easier to achieve without loopholes.
The standard syntax for formal self-arguments has a problem. The following is not possible, bacause the inner self-argument shadows the outer one:
Function.o = |f| |x| self(f(x))
One is forced to write instead:
Function.o = fn|f| g = self return |x| g(f(x)) end
This problem occurs often if one uses methods, because closures and higher order functions are frequently used. Now the idea is, to separate the self-argument via an semicolon from the other arguments. For actual arguments this syntax is already possible, but I will provide it also for formal arguments. Then we have:
Function.o = |g;f| |x| g(f(x))
What is the difference between what follows? Firstly:
m = load("m")
And secondly:
m = eval(read("m.moss"))
Behavior is different, because eval
returns a value rather than a module object. But the question that
comes into mind is: should they be equivalent? In order to achieve
that, in a module a module object should be returned explicitely rather
than implicitely. This would also solve another problem: How to
state a module that consists only of a single class or a single
function (e.g. to achieve advanced lazy loading and lazy
evaluation)? The problem here is an oddly looking import statement:
use class_name: class_name # vs. use class_name
Note that eval can be made quite powerful. It can
take an additional argument that specifies information about
the environment. For example, global variable of the environment
are used by default by eval. If a module would be loaded,
eval had to take an empty environment.
The interpreter already supports default arguments for
build in functions. Now a function's argument count can simply be
a range. Not given arguments will be filled out with
null. Now
function f(x,y=expression)
is simply syntatic sugar for
function f(x,y=null) if y is null then y=expression end
An implementation is straightforward:
Now construct (or compile in this order):
* block-node
* if-node-1
* if-node-2
...
* if-node-n
* body-node
Easy going. At next, default named arguments are stated as follows:
function f(x,m={})
a = m["a"] if "a" in m else a0
b = m["b"] if "b" in m else b0
# ...
end
That's clumsy. I believe, default named arguments are very important for usability and thus should be supported by the language. Now let
{a=a0, b=b0} = m
be syntactic sugar for
a = m["a"] if "a" in m else a0 b = m["b"] if "b" in m else b0
Without default arguments it should be more strict: Let
{a,b} = m
be syntactic sugar for
a = m["a"]; b = m["b"]
I call this the map unpacking statement.
It took me 100 lines of C code to implement map unpacking, including construction of a temporary variable if the right hand side is an expression. I think it was a worthwhile effort.
Finally it can be moved into the arguments list:
function f(x,{a=a0,b=b0})
# ...
end
as syntactic sugar for
function f(x,_m0_)
{a=a0,b=b0} = _m0_
# ...
end
Furthermore,
function f([x,y]) # ... end
is syntactic sugar for
function f(_t0_) x,y = _t0_ # ... end
In addition I achieved (by 30 lines of C code) syntactic sugar for named actual arguments:
f(x,y,a=e1,b=e2) ≡≡ f(x,y,{a=e1,b=e2})
They may appear in any order, independently from positional arguments. That is a little more welfare than simply omitting the curly brackets.
At first I recall that
begin ... end
is syntatic sugar for:
fn|| ... end()
Often we want to create a local variable, use it in one or more functions, and forget it afterwarts. Thus we want to have a local scope, so that the variable does not exist outside of this scope. In Moss I have used this ugly construction so far:
f = begin n = 42 return |x| n*x end
But if one wants to bind some value to more than one function, this construction becomes even more unpleasant:
f,g = begin n = 42 f = |x| n*x g = |x| x+n return f,g end
In Lua it is possible to restrict variables to a local scope:
do
local n = 42
function f(x)
return n*x
end
function g(x)
return x+n
end
end
print(f(2))
I did not realize until now that this is perfectly possible in my own programming language too:
begin global f,g n = 42 f = |x| n*x g = |x| x+n end print(f(2))
Furthermore, this actually solves the problem of having variables that are restricted to a module.1 And fortunately these variables can be accessed faster, since local variables are stored in a stack frame rather than the map of global variables.
A problem that remains is mutual recursion. In JavaScript this is solved by making it possible to use a local variable that is defined later on. For now, in Moss one would need to switch to global variables for this purpose.
Footnote 1: It would be possible to achieve that
a variable may be declared to be local to a module (module scope).
In C known as a static variable. Such a variable would also
be stored inside an array rather than a map. But to me
begin-end is nicer and more powerful as it leads
to more fine-grained constructions.
In Moss, a module, for example math, is made available by the following statement:
use math
The implementation so far was an internal import-function that added math to the map of global variables. A change to this behavior will be proposed now. The import-statement will be made syntactic sugar to:
math = load("math")
This has the advantage that math can be a local variable
now. We recapitulate that a private variable is a (can be modeled
as a) local variable of a block (in Moss: begin-end).
The full syntax is as follows:
# (A) use pathnode.pathnode.m: f,g # (B) use malias=pathnode.pathnode.m: falias=f, galias=g
This is defined to be syntactic sugar to:
# (A)
m = load("pathnode/pathnode/m")
f = m.f
g = m.g
# (B)
malias = load("pathnode/pathnode/m")
falias = malias.f
galias = malias.g
In Addition:
use m:*
# is meant to be
m = load("m")
gtab().update(record(m))
# and
use(m): f, g
# is meant to be (without load)
f = m.f; g = m.g
The assert statement was added to the language:
assert condition assert condition, text
It is implemented as syntatic sugar, because text
shall be lazily evaluated. So we have:
if not condition assertion_failed(text) end
Example of usage:
function pow(x,n)
assert n: Int and n>=0, "pow(x,n), n: Int, n>=0"
y=1
for k in 1..n
y=y*x
end
return y
end
print(pow(2,-2))
# Assertion failed: pow(x,n), n: Int, n>=0.
A failed assertion results in an ordinary exception that is shown together with a stack trace.
Update. Maybe it is a good idea to enable compilation
of assert statements only in debug mode. Debug mode will be
switched on by "moss -d". So, if something goes
wrong and a long strack trace is returned, debug mode could be
turned on to inspect the situation further.
If we have a string s, it is expensive to
create a slice s[i..j]. But as s is
immutable, a slice object could be returned, without copying data.
Now we can make every string a slice object, if we say we have a
immutable data array and a (pointer,len) to a part of it.
At first this contradicts with the string being a struct with a flexible array last member. We would need a double allocation. At next, the data array has to contain a reference counter. Ideally the data array is a struct with a flexible array last member. Not to forget that the string object itself needs an independet reference counter.
This sounds more complicated. So what have we won? Now we can take slices and slices of slices without the need of allocating and copying around data. Take into mind the basic algorithm that searches a substring in a string.
Interestingly this is an implementation detail that is transparent to the programming language because strings are chosen to be immutable.
Moving further, such a behavior is also interesting for
dynamic arrays (type List in Moss). If a slice
is obtained from an array, the arrays length should become immutable.
The information about immutable length, immutable data and
slicing can be modeled as an option type (extra behavior flag),
to separate it from the standard behavior. A problem is again,
that the data array needs an independent reference counter.
Alternatively, we could have a sum type (a tagged union) that chooses wether to point to data or to slice another array.
So, what have we won? Let's take a look on some naive algorithms:
# Naive quicksort qsort = |a| ([] if len(a)==0 else qsort(a[1..].filter(|x| x<a[0]))+[a[0]]+ qsort(a[1..].filter(|x| x>=a[0]))) # Naive sieve of Eratosthenes sieve = |a| ([] if len(a)==0 else [a[0]]+sieve(a[1..].filter(|x| x%a[0]!=0)))
Many huge copies are created by a[1..].
The algorithms could be made a bit more quick and memory
friendly, but it hardly is worthwhile as these algorithms are
terribly inefficient.
In Moss, the index operations a[i], m[key]
are strict. If i is out of bounds or key
is not found, an exception will be thrown. Now we could introduce
sloppy index operations a(i), a(key),
that return null if i is out of bounds or
key is not found. That's right, we simply overload the
function call operator.
Furthermore we introduce the null coalescing operator as
"a else b". Now these to statements are
semantically equivalent:
y = m[key] if key in m else x y = m(key) else x
In both statements, x is lazily evaluated.
In Moss, there is the member access operation "a.x".
One can have reflection this way:
y = record(a)["x"]
Here the problem emerges, that the ordinary index operation
does not respect the prototype chain. Now we find, that an
expression "a.x" is parsed into an AST
(dot a "x"). But the compiler
ever since the beginning was able to compile the more general
AST (dot a x) where a and x
are arbitray expressions. The recursive desecent may simply take an
atom after the dot. Thus I will introduce the general syntax
"a.(x)". So, adding very few lines to the compiler allows
us nice reflection with respect to the prototype chain. For clarity,
we have:
a.x ≡≡ a.("x")
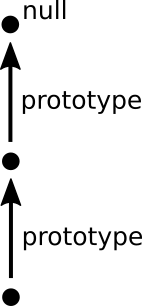
The basic idea for the object system of Moss is so far, that
the type and prototype of an object coincide. A property
(including methods) is searched in the object first,
then in the object's prototype, and then in the prototype's
prototype and so on until null is reached.
This simple model is shown by this graph:

Now, the problem arises that a type should have an own object-to-string method. But placed somewhere in the prototype chain, it will conflict with the object-to-string method for the type's instances. A solution is to obtain the object-to-string method from the object's type. But in order to do that, the type-prototype coincidence must be removed.
Now, the idea is, not to change the object system, but to patch the coincidence breakage into it. A table object is constructed as follows:
signature = prototype
t = table signature{x=value, y=value}
≡≡ table signature({x=value, y=value})
We can have multiple inheritance:
signature = [prototype1, prototype2, ..., prototypeN]
Now, a tuple is used to differentiate between a type and a prototype:
signature = (type, object_name, prototype)
This leads to the following model:
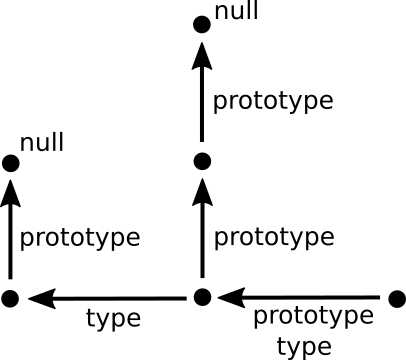
The patched type system looks as follows:
To make things easy, propterty access only searches the prototype chain. A complicated rule "one left then upwards" will not be used.
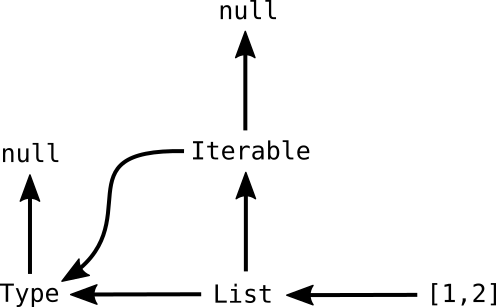
For object-to-string, the type name must be stored somewhere, and it should be easy to create a named class. For convenience the tuple is extended by optional elements. The complete signature is:
signature = (type, object_name, prototype, hidden_properties)
A simple example:
Bird = table(Type,"Bird"){
function string
"{} is a bird." % [self.name]
end,
function fly
"{} can fly!" % [self.name]
end
}
Duck = table(Type,"Duck",Bird){
function string
"{} is a duck." % [self.name]
end,
function dive
"{} can dive!" % [self.name]
end
}
d = table Duck{name = "Donald"}
print(d)
print(d.fly())
print(d.dive())
print("type: ", type(d))
# Output:
# Donald is a duck.
# Donald can fly!
# Donald can dive!
# type: Duck
Not posssible in Moss so far is proper lexical scoping.
Proper lexical scoping is a closure capture of an external local
variable from lexical scope by mutable reference. The local variable's
lifetime is increased from 'scope to
max('scope, 'closure).
In Moss, lexically scoped closures are possible, but by capture per cloning. Not possible so far is such a construct:
function main
s = 0
(1..4).each(fn|k|
s = s+k
end)
print(s)
end
The outer and inner s are two different variables
because of a cloning at closure creation. Thus, the outer
s will not be modified. How to solve this problem?
At first let me explain how I implemented closures. I will use
f = |x,y| |z| x+y+z
as an example to examine what is happening. This is transformed into the following pseudo-Moss:
f = fn|x,y| _t = [x,y] return fn(_t)|z| t[0]+t[1]+z end end
After transformation one can see why nothing happens:
function main
s = 0
_t = [s]
(1..4).each(fn(_t)|k|
_t[0] = _t[0]+k
end)
print(s)
end
Now, the idea is to regard the situation as a move of
s into _t. Thus also in outer scope,
we need to replace every occurence of a captured variable
by _t[i]. In this case, print(s)
is replaced by print(_t[0]).
Closure chains are not problematic:
function main
s = 0
_t = [s]
(1..4).each(fn(_t)|k|
_t[0] = _t[0]+k
end)
_t = [_t[0]]
(1..4).each(fn(_t)|k|
_t[0] = _t[0]+k
end)
print(_t[0])
end
Closure nesting is more problematic:
function main
s = 0
_t1 = [s]
(1..4).each(fn(_t1)|i|
_t2 = [_t1[0]]
(1..4).each(fn(_t2)|j|
_t2[0] = _t2[0]+i*j
end)
# lifetime of _t2 ends here
end)
print(_t2[0])
end
This is not possible, because the lifetime of _t2
is not long enough. There is more than one possible solution
to this problem. We have to take in mind that all of this
is about lexical scoping. Because of this situation, we could
simply move _t2 into the outmost local scope:
function main
s = 0
_t1 = [s]
_t2 = []
(1..4).each(fn(_t1)|i|
_t2.push(_t1[0])
(1..4).each(fn(_t2)|j|
_t2[0] = _t2[0]+i*j
end)
end)
print(_t2[0])
end
Again, difficulties arise when nesting and chaining are combined.
For convenience, in some higher order functions there was automatic list unpacking:
scalar_product = |v,w| zip(v,w).sum(|x,y| x*y)
= |v,w| zip(v,w).sum(|t| t[0]*t[1])
This is not possible in general and thus is removed in favor of explicit unpacking:
scalar_product = |v,w| zip(v,w).sum(|[x,y]| x*y)
For argument list unpacking there was so far:
f(1,2) ≡≡ f.apply([1,2])
This approach has the drawback that self arguments must be given explicitly:
x.m(1,2) ≡≡ x.m.apply(x;[1,2]) /*but not*/ x.m.apply([1,2])
Due to this reason, f.apply(a) is replaced
by f(*a).
Surprisingly, the implementation patch
was very short and took me only 30 min. I added the unary prefix operator
"*" to the recursive descent at the same level
as the unary perfix operators "+ - ~". Now in AST
compilation we match splat in these ASTs:
(apply f (splat (list 1 2))), (apply (dot x "m") (splat (list 1 2))), (apply (dot x "m") x (splat (list 1 2))),
and branch to compilation of unpacking apply. There we take
explicit and implicit self arguments into account again.
A new byte code APPLY is added to the interpreter.
This byte code calls a very short function that takes
f,self,a from the stack and calls the Rust-Moss
transition env.call(f,self,a) where env
is a pointer to the calling environment. The very same behavior
was in f.apply(self,a).
In before I mused about alternative approaches. One could have unpacked to the object stack and taken a dynamic argument count from the object stack. But firstly this would have made calling slower and secondly would have lead to stack overflow in case of large lists.
The following behavior is not implemented at this point of time:
f(*a,*b) ≡≡ f(*(a+b)), f(x,y,*a) ≡≡ f(*([x,y]+a)) etc.
Thus we need to use the right hand side.
The function call
object(prototype,properties)
is replaced by
table prototype(properties)
Thus we have
T = table{}
m = {x=1,y=2}
table{x=1,y=2} ≡≡ table null(m)
table T{x=1,y=2} ≡≡ table T(m)
In the last week I mused about adding generator comprehensions to the language. From that we receive list, set and dictionary comprehensions as a gift.
The most simple implementation is reduction to syntactic sugar. For example
list(f(x) for x in a)
will be transformed into:
list(fn*|| for x in a do yield f(x) end end)
The more complicated expression
list(f(x,y) for x in a if p(x) for y in b if q(x,y))
will be transformed into:
list(fn*||
for x in a
if p(x)
for y in b
if q(x,y)
yield f(x,y)
end
end
end
end
end)
This could be done directly during syntactic analysis, and done elegantly, the compiler would become only slightly slightly larger by 100 up to 200 lines.
After musing for some time about a capability based security model, I decided to compose a model of irreversible restrictions instead.
Capabilities are the most fine grained model, but are complicated to use because a system environment object has to be given to every function that shall have rights for system access. And this object has to be invisible for other functions. It would be a security hole, if this object is a global variable that could be made visible by an untrusted module.
Because of the emerging complexity, I decided to use a simpler
security model, which allows system access in the old fashion.
Basically, every system access needs to have a capability (a right,
a permission), which is stored in rte, the internal
runtime environment used in the interpreter. As per default, any file
can be read, but all other system access is prohibited. But running
"moss -unsafe" instead of "moss" enters
root mode, allowing for everything. Now, calls to the runtime system
(ordinary Moss functions) place irreversible restriction locks,
that cannot be unlocked anymore. There might be different of such
locks, for example for running shell commands, writing/reading
files, network access and so on. Note that unrestricted call of
shell commands implies writing files and network access too.
If such first few lines of a Moss program are written in a standard style, it is very easy to reason about what the program is allowed to and what not. The interface that these few lines provide, should be as easy and failure tolerant as possible. All default parameters should perform the most restriction.
The insistent drawback of this system is, that it is insecure to load untrusted modules in an authorized program. That is, one cannot have untrusted modules and authorization at the same time.
So, implementing custom getters and setters is not very diffecult,
as I have found. Basicly one provides a new class object from
a class constructor, but this is an Object::Interface
instead of an Object::Table. Let me explain,
Interface is the residual enum variant that contains
a dyn trait pointer, i.e. is the interface to all differnt kinds
of objects, for example long integers, multidimensional arrays,
file objects etc.
If a table object has such a class object A as its
prototype, the behavior of the dot operator will be determined by
methods of A. Ideally, the additional behavior is shadowed
by a branch on Object::Interface, i.e. against a simple
integer loaded from a pointer. That's a very small runtime penalty.
Implementing custom destructors is more difficult. Here the
problem arises that function calls need a reference to the calling
environment env. This reference must be given as an
argument to the destructor. But objects are designed to be destructed
everywhere. A custom Drop may be implemented, but
drop takes no additional arguments. Linear typing could
provide additional arguments, but this leads to very ugly code
and changes the overall design.
The solution I came up with is as follows. A class object
A contains an Rc-pointer to the runtime environment
rte. If an object is a child of A, by
calling drop it will be stored togehter with its
destructor in a buffer inside of rte. A flag of type
Cell<bool> inside of rte will be
set, indicating a non-empty buffer. Now, when returning from a
function, after a branch on the flag, the delayed destructions
are processed, because we have access to env.
But note, branching at this point is particularly time critical.
Any additional code will affect the calling mechanism and thus
the general interpreter performance. So, one branch on a
Cell<bool> behind a pointer to a struct
is bearable, but not more. But wait, we can do better.
To circumvent this, there is a slight modification of this technique.
A secondary calling environment will be stored inside of
rte. A flag in rte indicates whether
we are in a root destructor. All custom sub-destructions will be
stored in the buffer. After returning from all drops, the buffer will
be processed in the root destructor with the secondary calling
environment. We need to do it this way, because otherwise
sub-destructions would need a third calling environment,
sub-sub-destructions a fourth calling environment and so on.
Don't get confused, but I would consider it somewhat similar
to trampolining tail calls.
A typed programming language Moss is planned, the compiler producing Moss byte code. The syntax will be so similar that both languages will have the same file extension. The typed Moss will only have a few more keywords. For comparison, an example:
function map(a,f)
b = []
for x in a
b.push(f(x))
end
return b
end
function map[X,Y,n](a: List[X,n], f: X=>Y): List[Y,n];
let mut b: List[Y] = [];
for x in a do
b.push(f(x));
end
return b;
end
The dynamic Moss is actually more general, emulated by:
function map(a: List[Object], f: Object=>Object): List[Object];
let mut b: List[Object] = [];
for x in a do
b.push(f(x));
end
return b;
end
Another example:
let qsort[T: Ord, n](a: List[T,n]): List[T,n] =
[] if a==[] else
qsort(a[1..].filter(|x| x<a[0]))+[a[0]]+
qsort(a[1..].filter(|x| x>=a[0]));
Checking for leftover named arguments was very unergonomic so far.
The most flexible design I have figured out employs a wrapper type
Drain, which depletes the argument map by operator
overloading. This approach is also compatible with default arguments.
use unpack: drain, assert_empty
argm = {x=1,y=2,z=3}
{x,y} = drain(argm)
assert_empty(argm)
# Value error: unexpected named arguments: {"z": 3}.
The unpacking may be splitted into parts:
argm = {x=1,y=2}
dargm = drain(argm)
{x} = dargm
{y} = dargm
assert_empty(argm)
The unpacking may drain a copy, leaving the original argument map untouched:
m = copy(argm)
{x,y} = drain(m)
assert_empty(m)