| ↑ Up |
use math: nan, floor
# By equidistant nodes
# [x0+k*d, y[k]]
function pli(x0,d,y)
n = len(y)
return fn|x|
k = int(floor((x-x0)/d))
if k<0 or k+1>=n
return nan
else
return y[k]+(y[k+1]-y[k])/d*(x-x0-k*d)
end
end
end
# The first derivative of a function f at x diffh = |h| |f,x| (f(x+h)-f(x-h))/(2*h) diff = diffh(0.001) # Differential operator Dh = |h| |f| |x| (f(x+h)-f(x-h))/(2*h) D = Dh(0.001) f = |x| x^2 f1 = D(f) f2 = (D^2)(f)
function simpson(f,a,b,n)
h = (b-a)/n
y = 0
for i in 0..n-1
x = a+h*i
y = y+f(x)+4*f(x+0.5*h)+f(x+h)
end
return y*h/6
end
# Gauss-Legendre quadrature nodes,
# GL8 = [x[k],w[k]] for k in 0..7
GL8 = [
[-0.9602898564975362, 0.1012285362903764],
[-0.7966664774136267, 0.2223810344533745],
[-0.5255324099163290, 0.3137066458778874],
[-0.1834346424956498, 0.3626837833783619],
[ 0.1834346424956498, 0.3626837833783619],
[ 0.5255324099163290, 0.3137066458778874],
[ 0.7966664774136267, 0.2223810344533745],
[ 0.9602898564975362, 0.1012285362903764]
]
function gauss(f,a,b,n)
h = (b-a)/n
p = 0.5*h
s = 0
for j in 0..n-1
q = p+a+j*h
sj = 0
for t in GL8
sj += t[1]*f(p*t[0]+q)
end
s += p*sj
end
return s
end
# piecewise linear interpolation
use math.na: pli
# y'(x) = f(x,y(x))
# h: step size
# N: number of steps
function euler(f,{x0,y0,h,N})
x = x0; y = y0
a = [y]
for k in 1..N
y = y+h*f(x,y)
x = x0+k*h
a.push(y)
end
return pli(x0,h,a)
end
# y^(m)(x) = f(x,y)
# y = [y(x),y'(x),...,y^(m-1)(x)]
function euler_any_order(f,{x0,y0,h,N})
x = x0; y = copy(y0)
m = len(y)
a = [y[0]]
for k in 1..N
hf = h*f(x,y)
for i in 0..m-2
y[i] = y[i]+h*y[i+1]
end
y[m-1] = y[m-1]+hf
x = x0+k*h
a.push(y[0])
end
return pli(x0,h,a)
end
exp = euler(|x,y| y,{
x0=0, y0=1, h=0.01, N=1000
})
sin = euler_any_order(|x,y| -y[0],{
x0=0, y0=[0,1], h=0.01, N=1000
})
use svg.plotlib: system
use math.ode: runge_kutta
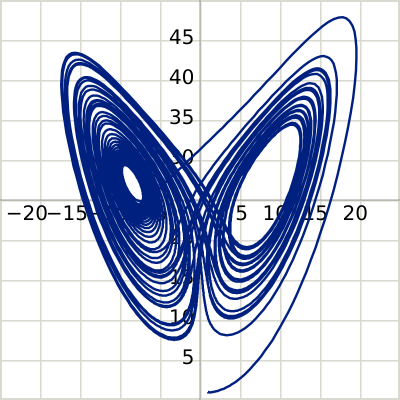
# Lorenz attractor
x,y,z = runge_kutta({
f = |t,[x,y,z]| [
10*(y-x),
x*(28-z)-y,
x*y-8/3*z
],
t0=0, y0 = [1,1,1],
w=40, unilateral = true
})
s = system(wx=25, wy=25, py=25)
s.vplot(|t| [x(t),z(t)], {t0=0, t1=40, n=200})
print(s.flush())

use plotlib: system
use math.la: vector
use math.ode: runge_kutta
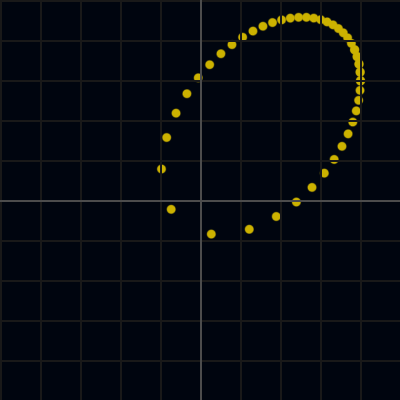
# Motion around a fixed center of mass,
# by Newton's law of gravitation:
# x''(t) = -GM*x/|x|^3.
G=1; M=1
x,v = runge_kutta({
f = |t,[x,v]| [v, -G*M*x/abs(x)^3],
y0 = [vector(4,3),vector(0,0.28)],
t0 = 0, h=0.01, w=100,
unilateral = true
})
s = system(dark = true, w=400, h=400, scale=2)
s.animate(fn|tstep|
t = 40*tstep
s.scatter([x(t)])
end, clear = false)
s.idle()
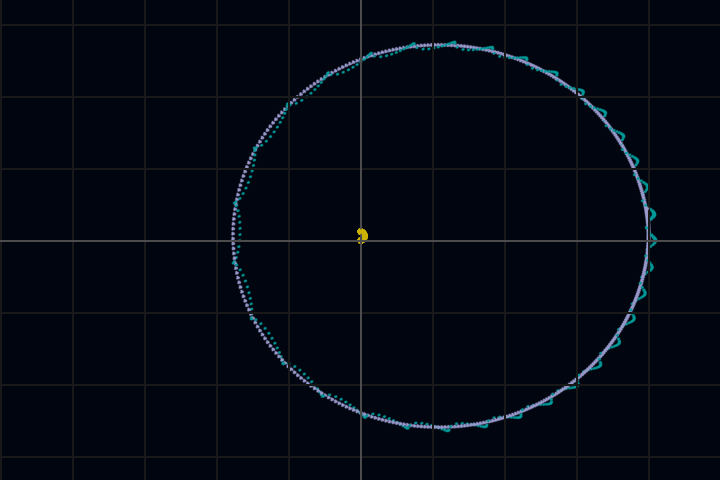
# n-body simulation,
# by Newton's law of gravitation:
# x[i]''(t) = G*sum(k!=i) m[k]*(x[k]-x[i])/|x[k]-x[i]|^3.
use plotlib: system
use math.la: vector
use math.ode: runge_kutta
function nbody({G,m})
n = len(m)
vindex = vector(*list(0..n-1))
return |x| vindex.map(|i| G*(0..n-1).sum(|k|
vector(0,0) if k==i else
m[k]*(x[k]-x[i])/abs(x[k]-x[i])^3))
end
m,x0,v0 = list(zip(
# Star
[1, vector(0,0), vector(0,0)],
# Planet
[0.01, vector(4,0), vector(0,0.4)],
# Moon
[0.0001, vector(4.1,0), vector(0,0.2)]
))
x0 = vector(*x0)
v0 = vector(*v0)
g = nbody(G=1,m=m)
x,v = runge_kutta({
f = |t,[x,v]| [v,g(x)],
y0 = [x0,v0],
t0 = 0, h=0.01, w=100,
unilateral = true
})
s = system(dark = true, w=720, h=480, scale=2)
s.animate(fn|tstep|
t = 4*tstep
xt = x(t)
s.scatter([xt[0]], radius=0.002)
s.rgb(0.6,0.6,0.8)
s.scatter([xt[1]], radius=0.001)
s.rgb(0,0.6,0.6)
s.scatter([xt[2]], radius=0.0005)
end, clear = false)
s.idle()
use math: pi, exp
# Fast Fourier transform of a.
# Note: len(a) is a power of two.
function fft(a)
if len(a)<=1
return copy(a)
else
even = fft(a[0..:2]); odd = fft(a[1..:2])
N = len(a); L = list(0..N//2-1)
T = L.map(|k| exp(-2i*pi*k/N)*odd[k])
return (L.map(|k| even[k]+T[k])+
L.map(|k| even[k]-T[k]))
end
end
What follows is an approximation of the complex Riemann zeta function ζ(s) by an application of the Euler-MacLaurin formula, which yields:
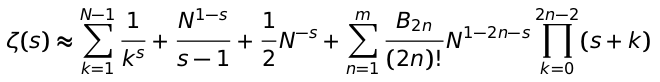
At next this calculation will be implemented without further ado. Finally the functional equation of the zeta function (a.k.a. reflection formula) is used for Re(s)<0.
use math: pi, sin, gamma
use math.sf: B
use cmath: re
function new_zeta({N,m})
function Euler_MacLaurin_term(s,N,m)
return (1..m).sum(|n| B(2*n)/gamma(2*n+1)
*N^(1-2*n-s)*(0..2*n-2).prod(|k| (s+k)))
end
function zeta_Euler_MacLaurin(s,N,m)
return ((1..N-1).sum(|k| 1/k^s)+N^(1-s)/(s-1)
+0.5*N^(-s)+Euler_MacLaurin_term(s,N,m))
end
return fn zeta|s|
if re(s)<0
return (2^s*pi^(s-1)*sin(pi*s/2)
*gamma(1-s)*zeta_Euler_MacLaurin(1-s,N,m))
else
return zeta_Euler_MacLaurin(s,N,m)
end
end
end
zeta = new_zeta(N=12,m=6)