x=a
a==b
x^n
a[i]
a%m
not a
a and b, a or b
x in A
A<=B, A<B
A&B, A|B
A-B, A$B
(0..), (1..)
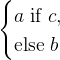
a if c else b
|x| 2*x
(f^n)(x)
{a,b,c}
[a,b,c]
A*B, A^n
| ↑ Up |
There are a number of notations similar to mathematical notation.
| Math | Moss | Notes |
|---|---|---|
| x := a | x=a
| assignment |
| a = b | a==b
| comparison |
| xn | x^n
| to the power of |
| ai | a[i]
| index |
| a mod m | a%m
| modulo |
| ¬a | not a
| logical negation |
| a∧b, a∨b | a and b, a or b
| logical and, or |
| x ∈ A | x in A
| is an element of |
| A⊆B, A⊂B | A<=B, A<B
| subset, proper subset |
| A∩B, A∪B | A&B, A|B
| intersection, union |
| A\B, AΔB | A-B, A$B
| difference, symmetric difference |
| N0, N* | (0..), (1..)
| non-negative integers, positive integers |
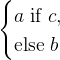
| a if c else b | distinction of cases |
| x ↦ 2x | |x| 2*x
| anonymous function |
| fn(x) | (f^n)(x)
| iterated function |
| {a, b, c} | {a,b,c}
| sets |
| (a, b, c) | [a,b,c]
| tuples |
| A×B, An | A*B, A^n
| cartesian product, power |
Furthermore:
| Math | Moss | Notes |
|---|---|---|
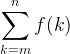
| (m..n).sum(|k| f(k)) | summation over a range |
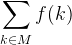
| M.sum(|k| f(k)) | summation over an iterable object |
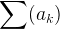
| a.sum() | summation |
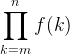
| (m..n).prod(|k| f(k)) | product over a range |
| ∀x∈M(p(x)) | M.all(|x| p(x))
| universal quantifier |
| ∃x∈M(p(x)) | M.any(|x| p(x))
| existential quantifier |
| {x∈M | p(x)} | M.filter(|x| p(x))
| set builder notation |
| #{x∈M | p(x)} | M.count(|x| p(x))
| counting |
| f(A) | f[A]
| image of a function |
use math: sqrt, root use math.na: inv, diffh, integral use cmath: conj, re, im diff = diffh(order=false)
| Math | Moss | Notes |
|---|---|---|
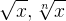
| sqrt(x), root(n,x)
| square root and general root |
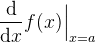
| diff(f,a) | derivative |
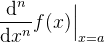
| diff(f,a,n) | derivative of order n |
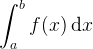
| integral(a,b,|x| f(x)) | definite integral |
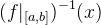
| inv(f,x,a,b)
| inverse function |
| a+bi | a+b*1i
| complex numbers |
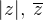
| abs(z), conj(z)
| absolute value, conjugation |
| Re z, Im z | re(z), im(z)
| real part, imaginary part |
There are different forms of integer division.
# Floor division div_floor = |x,y| x//y mod_floor = |x,y| x%y # Euclidean division div_euc = |x,y| sgn(y)*(x//abs(y)) mod_euc = |x,y| x%abs(y) # Truncating division div_trunc = |x,y| sgn(x)*sgn(y)*(abs(x)//abs(y)) mod_trunc = |x,y| x%(sgn(x)*abs(y))
In case of y>0, flooring division and Euclidean
division coincide. In case of x>0 and
y>0, all of them coincide.
Furthermore, there are floating point counterparts:
use math: floor, trunc # Floor division div_floor = |x,y| floor(x/y) mod_floor = |x,y| x-y*floor(x/y) # Euclidean division div_euc = |x,y| sgn(y)*floor(x/abs(y)) mod_euc = |x,y| x-abs(y)*floor(x/abs(y)) # Truncating division div_trunc = |x,y| trunc(x/y) mod_trunc = |x,y| x-y*trunc(x/y)
Module math.rational provides rational numbers.
A rational number a/b is denoted as
rat(a,b).
> use math.rational: rat > rat(1,2)+2 5/2 > rat(4,5)^40+rat(2,3)^20 13752006853860928837764998235160576/ 31712119389339932240545749664306640625
You can check this with the computer algebra system Maxima:
(%i1) (4/5)^40+(2/3)^20;
13752006853860928837764998235160576
(%o1) --------------------------------------
31712119389339932240545749664306640625
Main chapter: Linear algebra.
Module math.la provides vector algebra.
use math.la: vector, matrix v = vector(1,2) A = matrix( [1,2], [3,4] ) print(A*v)