# orx-split-vec
[](https://crates.io/crates/orx-split-vec)
[](https://docs.rs/orx-split-vec)
An efficient constant access time vector with dynamic capacity and pinned elements.
## A. Motivation
There are various situations where pinned elements are critical.
* It is critical in enabling **efficient, convenient and safe self-referential collections** with thin references, see [`SelfRefCol`](https://crates.io/crates/orx-selfref-col) for details, and its special cases such as [`LinkedList`](https://crates.io/crates/orx-linked-list).
* It is important for **concurrent** programs as it eliminates safety concerns related with elements implicitly carried to different memory locations. This helps reducing and dealing with the complexity of concurrency, and leads to efficient concurrent data structures. See [`ConcurrentIter`](https://crates.io/crates/orx-concurrent-iter), [`ConcurrentBag`](https://crates.io/crates/orx-concurrent-bag) or [`ConcurrentOrderedBag`](https://crates.io/crates/orx-concurrent-ordered-bag) for such concurrent data structures which are conveniently built on the pinned element guarantees of pinned vectors.
* It is essential in allowing an **immutable push** vector; i.e., [`ImpVec`](https://crates.io/crates/orx-imp-vec). This is a very useful operation when the desired collection is a bag or a container of things, rather than having a collective meaning. In such cases, `ImpVec` allows avoiding certain borrow checker complexities, heap allocations and wide pointers such as `Box` or `Rc` or etc.
## B. Comparison with `FixedVec`
[`FixedVec`](https://crates.io/crates/orx-fixed-vec) is another [`PinnedVec`](https://crates.io/crates/orx-pinned-vec) implementation aiming the same goal but with different features. You may see the comparison in the table below.
| **`FixedVec`** | **`SplitVec`** |
|------------------------------------------------------------------------------|----------------------------------------------------------------------------------|
| Implements `PinnedVec` => can be wrapped by an `ImpVec` or `SelfRefCol` or `ConcurrentBag`, etc. | Implements `PinnedVec` => can as well be wrapped by them. |
| Requires exact capacity to be known while creating. | Can be created with any level of prior information about required capacity. |
| Cannot grow beyond capacity; panics when `push` is called at capacity. | Can grow dynamically. Further, it provides control on how it must grow. |
| It is just a wrapper around `std::vec::Vec`; hence, has equivalent performance. | Performance-optimized built-in growth strategies also have `std::vec::Vec` equivalent performance. |
After the performance optimizations on the `SplitVec`, it is now comparable to `std::vec::Vec` in terms of performance (see E. Benchmarks for the experiments). This might make `SplitVec` a dominating choice over `FixedVec`.
## C. Growth with Pinned Elements
As the name suggests, `SplitVec` is a vector represented as a sequence of multiple contagious data fragments.
The vector is said to be at its capacity when all fragments are completely utilized. When the vector needs to grow further while at capacity, a new fragment is allocated. Therefore, growth does not require copying memory to a new memory location. Already pushed elements stay pinned to their memory locations.
### C.1. Available Growth Strategies: **`Linear` | `Doubling` | `Recursive`**
The capacity of the new fragment is determined by the chosen growth strategy. Assume that `vec: SplitVec<_, G>` where `G: Growth` contains one fragment of capacity `C`, which is also the capacity of the vector since it is the only fragment. Assume, we used up all capacity; i.e., `vec.len() == vec.capacity()` (`C`). If we attempt to push a new element, `SplitVec` will allocate the second fragment with the following capacity:
| **`Growth`** Strategy | 1st Fragment Capacity | 2nd Fragment Capacity | Vector Capacity |
|-----------------------------------------|-----------------------|-----------------------|-----------------|
| `Linear` | `C` | `C` | `2 * C` |
| `Doubling` | `C` | `2 * C` | `3 * C` |
`C` is set on initialization as a power of two for `Linear` strategy, and it is fixed to 4 for `Doubling` strategy to allow for access time optimizations.
In addition there exists the `Recursive` growth strategy, which behaves as the `Doubling` strategy at the beginning. However, it allows for zero-cost `append` operation at the expense of a reduced random access time performance.
Growth strategies which allow for constant time random access additionally implement the `GrowthWithConstantTimeAccess` trait, which are currently `Doubling` and `Linear` strategies.
Please see the E. Benchmarks section for tradeoffs and details. The summary is as follows:
* Use `SplitVec` (or equivalently `SplitVec`)
* when it is required to have pinned elements and we need close to standard vector serial and random access performance, or
* when the elements are large and we don't have good capacity estimates, so that we can benefit from split vector's no-copy growth
* Use `SplitVec`
* when it is required to have pinned elements and we need close to standard vector serial access performance while it is okay to have slower random access performance, or
* when `append`ing other vectors or split vectors is a frequent and important operation.
* Use `SplitVec` when we have a good idea on the chunk size of the growth to reduce impact of wasted capacity with doubling of `std::vec::Vec` or `Doubling` or `Recursive`.
### C.2. Custom Growth Strategies
In order to define a custom growth strategy, one needs to implement the `Growth` trait. Implementation is straightforward. The trait contains two methods. The following method is required:
```rust ignore
fn new_fragment_capacity(&self, fragments: &[Fragment]) -> usize
```
Notice that it takes as argument all already allocated fragments and needs to decide on the capacity of the new fragment.
The second method `fn get_fragment_and_inner_indices(&self, vec_len: usize, fragments: &[Fragment], element_index: usize) -> Option<(usize, usize)>` has a default implementation and can be overwritten if the strategy allows for efficient computation of the indices.
## D. Examples
### D.1. Usage similar to `std::vec::Vec`
```rust
use orx_split_vec::*;
let mut vec = SplitVec::new();
vec.push(0);
vec.extend_from_slice(&[1, 2, 3]);
assert_eq!(vec, &[0, 1, 2, 3]);
vec[0] = 10;
assert_eq!(10, vec[0]);
vec.remove(0);
vec.insert(0, 0);
assert_eq!(6, vec.iter().sum());
assert_eq!(vec.clone(), vec);
let std_vec: Vec<_> = vec.into();
assert_eq!(&std_vec, &[0, 1, 2, 3]);
```
### D.2. `SplitVec` Specific Operations
```rust
use orx_split_vec::*;
#[derive(Clone)]
struct MyCustomGrowth;
impl Growth for MyCustomGrowth {
fn new_fragment_capacity_from(&self, fragment_capacities: impl ExactSizeIterator- ) -> usize {
fragment_capacities.last().map(|f| f + 1).unwrap_or(4)
}
}
impl PseudoDefault for MyCustomGrowth {
fn pseudo_default() -> Self {
MyCustomGrowth
}
}
// set the growth explicitly
let vec: SplitVec = SplitVec::with_linear_growth(4);
let vec: SplitVec = SplitVec::with_doubling_growth();
let vec: SplitVec = SplitVec::with_growth(MyCustomGrowth);
// methods revealing fragments
let mut vec = SplitVec::with_doubling_growth();
vec.extend_from_slice(&[0, 1, 2, 3]);
assert_eq!(4, vec.capacity());
assert_eq!(1, vec.fragments().len());
vec.push(4);
assert_eq!(vec, &[0, 1, 2, 3, 4]);
assert_eq!(2, vec.fragments().len());
assert_eq!(4 + 8, vec.capacity());
// SplitVec is not contagious; instead a collection of contagious fragments
// so it might or might not return a slice for a given range
let slice: SplitVecSlice<_> = vec.try_get_slice(1..3);
assert_eq!(slice, SplitVecSlice::Ok(&[1, 2]));
let slice = vec.try_get_slice(3..5);
// the slice spans from fragment 0 to fragment 1
assert_eq!(slice, SplitVecSlice::Fragmented(0, 1));
let slice = vec.try_get_slice(3..7);
assert_eq!(slice, SplitVecSlice::OutOfBounds);
// or the slice can be obtained as a vector of slices
let slices = vec.slices(0..3);
assert_eq!(1, slices.len());
assert_eq!(slices[0], &[0, 1, 2]);
let slices = vec.slices(3..5);
assert_eq!(2, slices.len());
assert_eq!(slices[0], &[3]);
assert_eq!(slices[1], &[4]);
let slices = vec.slices(0..vec.len());
assert_eq!(2, slices.len());
assert_eq!(slices[0], &[0, 1, 2, 3]);
assert_eq!(slices[1], &[4]);
```
### D.3. Pinned Elements
Unless elements are removed from the vector, the memory location of an element already pushed to the `SplitVec` never changes unless explicitly changed.
```rust
use orx_split_vec::*;
let mut vec = SplitVec::new(); // Doubling growth as the default strategy
// split vec with 1 item in 1 fragment
vec.push(42usize);
assert_eq!(&[42], &vec);
assert_eq!(1, vec.fragments().len());
assert_eq!(&[42], &vec.fragments()[0]);
// let's get a pointer to the first element
let addr42 = &vec[0] as *const usize;
// let's push 3 + 8 + 16 new elements to end up with 3 fragments
for i in 1..(3 + 8 + 16) {
vec.push(i);
}
for (i, elem) in vec.iter().enumerate() {
assert_eq!(if i == 0 { 42 } else { i }, *elem);
}
// now the split vector is composed of 11 fragments each with a capacity of 10
assert_eq!(3, vec.fragments().len());
// the memory location of the first element remains intact
assert_eq!(addr42, &vec[0] as *const usize);
// we can safely dereference it and read the correct value
// dereferencing is still unsafe for SplitVec,
// but the underlying guarantee will be used by wrappers such as ImpVec or SelfRefCol
assert_eq!(unsafe { *addr42 }, 42);
```
## E. Benchmarks
Recall that the motivation of using a split vector is to get benefit of the pinned elements and to avoid standard vector's memory copies in very specific situations; rather than to be a replacement. The aim of performance optimizations and benchmarks is to make sure that performance of critical operations is kept within desired ranges. `SplitVec` seems to satisfy this. After optimizations, built-in growth strategies appear to have a similar performance to `std::vec::Vec` in growth, serial access and random access benchmarks, and a better performance in append benchmarks.
*You may find the details of each benchmark in the following subsections. All the numbers in tables below represent duration in milliseconds.*
### E.1. Grow
*You may see the benchmark at [benches/grow.rs](https://github.com/orxfun/orx-split-vec/blob/main/benches/grow.rs).*
The benchmark compares the build up time of vectors by pushing elements one by one. The baseline is the vector created by `std::vec::Vec::with_capacity` which has the perfect information on the number of elements to be pushed. The compared variants are vectors created with no prior knowledge about capacity: `std::vec::Vec::new`, `SplitVec<_, Linear>` and `SplitVec<_, Doubling>`.
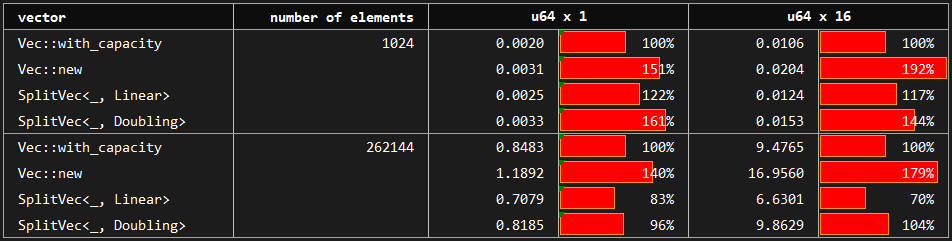 The baseline **std_vec_with_capacity** performs between 1.5 and 2.0 times faster than **std_vec_new** which has no capacity information and requires copies while growing. As mentioned before, **`SplitVec`** growth is copy-free guaranteeing that pushed elements stay pinned. Therefore, it is expected to perform in between. However, it performs almost as well as, and sometimes faster than, std_vec_with_capacity.
*`Recursive` strategy is omitted here since it behaves exactly as the `Doubling` strategy. For its differences, please see random access and append benchmarks.*
### E.2. Random Access
*You may see the benchmark at [benches/random_access.rs](https://github.com/orxfun/orx-split-vec/blob/main/benches/random_access.rs).*
In this benchmark, we access vector elements by indices in a random order. Here the baseline is again the standard vector created by `Vec::with_capacity`, which is compared with `Linear` and `Doubling` growth strategies of the `SplitVec` which are optimized specifically for the random access. Furthermore, `Recursive` growth strategy which does not provide constant time random access operation is included in the benchmarks.
Note that `Recursive` uses the `Growth` trait's default `get_fragment_and_inner_indices` implementation, and hence, reflects the expected random access performance of custom growth strategies without a specialized access method.
The baseline **std_vec_with_capacity** performs between 1.5 and 2.0 times faster than **std_vec_new** which has no capacity information and requires copies while growing. As mentioned before, **`SplitVec`** growth is copy-free guaranteeing that pushed elements stay pinned. Therefore, it is expected to perform in between. However, it performs almost as well as, and sometimes faster than, std_vec_with_capacity.
*`Recursive` strategy is omitted here since it behaves exactly as the `Doubling` strategy. For its differences, please see random access and append benchmarks.*
### E.2. Random Access
*You may see the benchmark at [benches/random_access.rs](https://github.com/orxfun/orx-split-vec/blob/main/benches/random_access.rs).*
In this benchmark, we access vector elements by indices in a random order. Here the baseline is again the standard vector created by `Vec::with_capacity`, which is compared with `Linear` and `Doubling` growth strategies of the `SplitVec` which are optimized specifically for the random access. Furthermore, `Recursive` growth strategy which does not provide constant time random access operation is included in the benchmarks.
Note that `Recursive` uses the `Growth` trait's default `get_fragment_and_inner_indices` implementation, and hence, reflects the expected random access performance of custom growth strategies without a specialized access method.
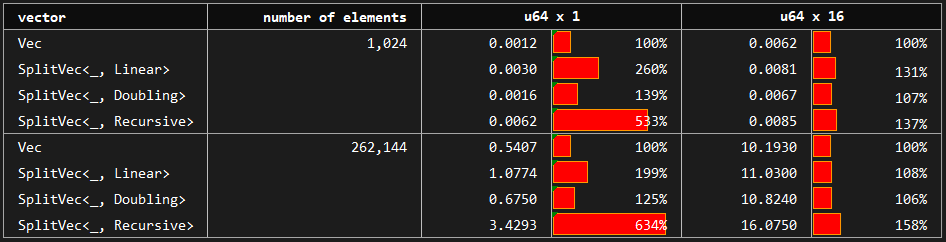 We can see that `Linear` is slower than `Doubling`. Random access performance of `Doubling` is at most 50% slower than the standard vector and the difference approaches to zero as the element size or number of elements gets larger.
`Recursive`, on the other hand, does not have constant time complexity for random access operation which can be observed in the table. It is between 4 and 7 times slower than the slower access for small elements and around 1.5 times slower for large structs. In order to make the tradeoffs clear and brief; `SplitVec<_, Recursive>` mainly differs from standard and split vector alternatives by random access performance (worse) and append performance (better).
### E.3. Serial Access
*You may see the benchmark at [benches/serial_access.rs](https://github.com/orxfun/orx-split-vec/blob/main/benches/serial_access.rs).*
Here, we benchmark the case where we access each element of the vector in order starting from the first element to the last. We use the same standard vector as the baseline. For completeness, baseline is compared with `Doubling`, `Linear` and `Recursive` growth strategies; however, `SplitVec` actually uses the same iterator to allow for the serial access for any growth strategy.
We can see that `Linear` is slower than `Doubling`. Random access performance of `Doubling` is at most 50% slower than the standard vector and the difference approaches to zero as the element size or number of elements gets larger.
`Recursive`, on the other hand, does not have constant time complexity for random access operation which can be observed in the table. It is between 4 and 7 times slower than the slower access for small elements and around 1.5 times slower for large structs. In order to make the tradeoffs clear and brief; `SplitVec<_, Recursive>` mainly differs from standard and split vector alternatives by random access performance (worse) and append performance (better).
### E.3. Serial Access
*You may see the benchmark at [benches/serial_access.rs](https://github.com/orxfun/orx-split-vec/blob/main/benches/serial_access.rs).*
Here, we benchmark the case where we access each element of the vector in order starting from the first element to the last. We use the same standard vector as the baseline. For completeness, baseline is compared with `Doubling`, `Linear` and `Recursive` growth strategies; however, `SplitVec` actually uses the same iterator to allow for the serial access for any growth strategy.
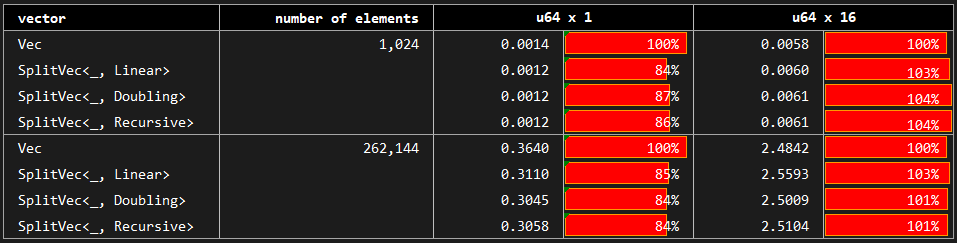 The results show that there are minor deviations but no significant difference between the variants.
### E.4. Append
*You may see the benchmark at [benches/serial_access.rs](https://github.com/orxfun/orx-split-vec/blob/main/benches/append.rs).*
Appending vectors to vectors might be a critical operation in certain cases. One example is the recursive data structures such as trees or linked lists or vectors themselves. We might append a tree to another tree to get a new merged tree. This operation could be handled by copying data to keep a certain required structure or by simply accepting the incoming chunk (no-ops).
* `std::vec::Vec<_>`, `SplitVec<_, Doubling>` and `SplitVec<_, Linear>` do the prior one in order to keep their internal structure which allows for efficient random access.
* `SplitVec<_, Recursive>`, on the other hand, utilizes its fragmented structure and follows the latter approach. Hence, appending another vector to it has no cost, simply no-ops. This does not degrade serial access performance. However, it leads to slower random access. Please refer to the corresponding benchmarks above.
The results show that there are minor deviations but no significant difference between the variants.
### E.4. Append
*You may see the benchmark at [benches/serial_access.rs](https://github.com/orxfun/orx-split-vec/blob/main/benches/append.rs).*
Appending vectors to vectors might be a critical operation in certain cases. One example is the recursive data structures such as trees or linked lists or vectors themselves. We might append a tree to another tree to get a new merged tree. This operation could be handled by copying data to keep a certain required structure or by simply accepting the incoming chunk (no-ops).
* `std::vec::Vec<_>`, `SplitVec<_, Doubling>` and `SplitVec<_, Linear>` do the prior one in order to keep their internal structure which allows for efficient random access.
* `SplitVec<_, Recursive>`, on the other hand, utilizes its fragmented structure and follows the latter approach. Hence, appending another vector to it has no cost, simply no-ops. This does not degrade serial access performance. However, it leads to slower random access. Please refer to the corresponding benchmarks above.
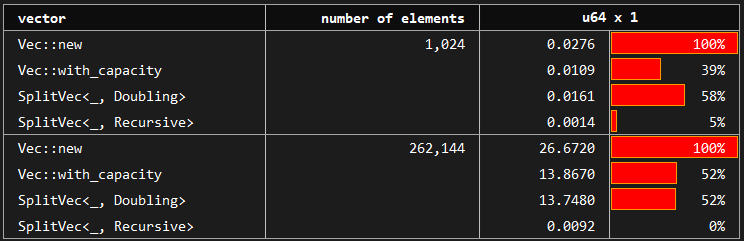 You may see that `SplitVec` (equivalently `SplitVec` using the default) is around twice faster than `std::vec::Vec` when we don't have any prior information about the required capacity. When we have perfect information and create our vector with `std::vec::Vec::with_capacity` providing the exact required capacity, `std::vec::Vec` and `SplitVec` perform equivalently. This makes `SplitVec` a preferable option.
`SplitVec` on the other hand is a different story allowing zero-cost appends which is independent of size of the data being appended.
## License
This library is licensed under MIT license. See LICENSE for details.
You may see that `SplitVec` (equivalently `SplitVec` using the default) is around twice faster than `std::vec::Vec` when we don't have any prior information about the required capacity. When we have perfect information and create our vector with `std::vec::Vec::with_capacity` providing the exact required capacity, `std::vec::Vec` and `SplitVec` perform equivalently. This makes `SplitVec` a preferable option.
`SplitVec` on the other hand is a different story allowing zero-cost appends which is independent of size of the data being appended.
## License
This library is licensed under MIT license. See LICENSE for details.
 The baseline **std_vec_with_capacity** performs between 1.5 and 2.0 times faster than **std_vec_new** which has no capacity information and requires copies while growing. As mentioned before, **`SplitVec`** growth is copy-free guaranteeing that pushed elements stay pinned. Therefore, it is expected to perform in between. However, it performs almost as well as, and sometimes faster than, std_vec_with_capacity.
*`Recursive` strategy is omitted here since it behaves exactly as the `Doubling` strategy. For its differences, please see random access and append benchmarks.*
### E.2. Random Access
*You may see the benchmark at [benches/random_access.rs](https://github.com/orxfun/orx-split-vec/blob/main/benches/random_access.rs).*
In this benchmark, we access vector elements by indices in a random order. Here the baseline is again the standard vector created by `Vec::with_capacity`, which is compared with `Linear` and `Doubling` growth strategies of the `SplitVec` which are optimized specifically for the random access. Furthermore, `Recursive` growth strategy which does not provide constant time random access operation is included in the benchmarks.
Note that `Recursive` uses the `Growth` trait's default `get_fragment_and_inner_indices` implementation, and hence, reflects the expected random access performance of custom growth strategies without a specialized access method.
The baseline **std_vec_with_capacity** performs between 1.5 and 2.0 times faster than **std_vec_new** which has no capacity information and requires copies while growing. As mentioned before, **`SplitVec`** growth is copy-free guaranteeing that pushed elements stay pinned. Therefore, it is expected to perform in between. However, it performs almost as well as, and sometimes faster than, std_vec_with_capacity.
*`Recursive` strategy is omitted here since it behaves exactly as the `Doubling` strategy. For its differences, please see random access and append benchmarks.*
### E.2. Random Access
*You may see the benchmark at [benches/random_access.rs](https://github.com/orxfun/orx-split-vec/blob/main/benches/random_access.rs).*
In this benchmark, we access vector elements by indices in a random order. Here the baseline is again the standard vector created by `Vec::with_capacity`, which is compared with `Linear` and `Doubling` growth strategies of the `SplitVec` which are optimized specifically for the random access. Furthermore, `Recursive` growth strategy which does not provide constant time random access operation is included in the benchmarks.
Note that `Recursive` uses the `Growth` trait's default `get_fragment_and_inner_indices` implementation, and hence, reflects the expected random access performance of custom growth strategies without a specialized access method.
 We can see that `Linear` is slower than `Doubling`. Random access performance of `Doubling` is at most 50% slower than the standard vector and the difference approaches to zero as the element size or number of elements gets larger.
`Recursive`, on the other hand, does not have constant time complexity for random access operation which can be observed in the table. It is between 4 and 7 times slower than the slower access for small elements and around 1.5 times slower for large structs. In order to make the tradeoffs clear and brief; `SplitVec<_, Recursive>` mainly differs from standard and split vector alternatives by random access performance (worse) and append performance (better).
### E.3. Serial Access
*You may see the benchmark at [benches/serial_access.rs](https://github.com/orxfun/orx-split-vec/blob/main/benches/serial_access.rs).*
Here, we benchmark the case where we access each element of the vector in order starting from the first element to the last. We use the same standard vector as the baseline. For completeness, baseline is compared with `Doubling`, `Linear` and `Recursive` growth strategies; however, `SplitVec` actually uses the same iterator to allow for the serial access for any growth strategy.
We can see that `Linear` is slower than `Doubling`. Random access performance of `Doubling` is at most 50% slower than the standard vector and the difference approaches to zero as the element size or number of elements gets larger.
`Recursive`, on the other hand, does not have constant time complexity for random access operation which can be observed in the table. It is between 4 and 7 times slower than the slower access for small elements and around 1.5 times slower for large structs. In order to make the tradeoffs clear and brief; `SplitVec<_, Recursive>` mainly differs from standard and split vector alternatives by random access performance (worse) and append performance (better).
### E.3. Serial Access
*You may see the benchmark at [benches/serial_access.rs](https://github.com/orxfun/orx-split-vec/blob/main/benches/serial_access.rs).*
Here, we benchmark the case where we access each element of the vector in order starting from the first element to the last. We use the same standard vector as the baseline. For completeness, baseline is compared with `Doubling`, `Linear` and `Recursive` growth strategies; however, `SplitVec` actually uses the same iterator to allow for the serial access for any growth strategy.
 The results show that there are minor deviations but no significant difference between the variants.
### E.4. Append
*You may see the benchmark at [benches/serial_access.rs](https://github.com/orxfun/orx-split-vec/blob/main/benches/append.rs).*
Appending vectors to vectors might be a critical operation in certain cases. One example is the recursive data structures such as trees or linked lists or vectors themselves. We might append a tree to another tree to get a new merged tree. This operation could be handled by copying data to keep a certain required structure or by simply accepting the incoming chunk (no-ops).
* `std::vec::Vec<_>`, `SplitVec<_, Doubling>` and `SplitVec<_, Linear>` do the prior one in order to keep their internal structure which allows for efficient random access.
* `SplitVec<_, Recursive>`, on the other hand, utilizes its fragmented structure and follows the latter approach. Hence, appending another vector to it has no cost, simply no-ops. This does not degrade serial access performance. However, it leads to slower random access. Please refer to the corresponding benchmarks above.
The results show that there are minor deviations but no significant difference between the variants.
### E.4. Append
*You may see the benchmark at [benches/serial_access.rs](https://github.com/orxfun/orx-split-vec/blob/main/benches/append.rs).*
Appending vectors to vectors might be a critical operation in certain cases. One example is the recursive data structures such as trees or linked lists or vectors themselves. We might append a tree to another tree to get a new merged tree. This operation could be handled by copying data to keep a certain required structure or by simply accepting the incoming chunk (no-ops).
* `std::vec::Vec<_>`, `SplitVec<_, Doubling>` and `SplitVec<_, Linear>` do the prior one in order to keep their internal structure which allows for efficient random access.
* `SplitVec<_, Recursive>`, on the other hand, utilizes its fragmented structure and follows the latter approach. Hence, appending another vector to it has no cost, simply no-ops. This does not degrade serial access performance. However, it leads to slower random access. Please refer to the corresponding benchmarks above.
 You may see that `SplitVec
You may see that `SplitVec