Non-physical operators which may be non-unitary, non-norm-preserving, even non-Hermitian. More...
Functions | |
| void | applyDiagonalOp (Qureg qureg, DiagonalOp op) |
Apply a diagonal operator, which is possibly non-unitary and non-Hermitian, to the entire qureg. More... | |
| void | applyFullQFT (Qureg qureg) |
Applies the quantum Fourier transform (QFT) to the entirety of qureg. More... | |
| void | applyMatrix2 (Qureg qureg, int targetQubit, ComplexMatrix2 u) |
| Apply a general 2-by-2 matrix, which may be non-unitary. More... | |
| void | applyMatrix4 (Qureg qureg, int targetQubit1, int targetQubit2, ComplexMatrix4 u) |
| Apply a general 4-by-4 matrix, which may be non-unitary. More... | |
| void | applyMatrixN (Qureg qureg, int *targs, int numTargs, ComplexMatrixN u) |
| Apply a general N-by-N matrix, which may be non-unitary, on any number of target qubits. More... | |
| void | applyMultiControlledMatrixN (Qureg qureg, int *ctrls, int numCtrls, int *targs, int numTargs, ComplexMatrixN u) |
| Apply a general N-by-N matrix, which may be non-unitary, with additional controlled qubits. More... | |
| void | applyMultiVarPhaseFunc (Qureg qureg, int *qubits, int *numQubitsPerReg, int numRegs, enum bitEncoding encoding, qreal *coeffs, qreal *exponents, int *numTermsPerReg) |
Induces a phase change upon each amplitude of qureg, determined by a multi-variable exponential polynomial "phase function". More... | |
| void | applyMultiVarPhaseFuncOverrides (Qureg qureg, int *qubits, int *numQubitsPerReg, int numRegs, enum bitEncoding encoding, qreal *coeffs, qreal *exponents, int *numTermsPerReg, long long int *overrideInds, qreal *overridePhases, int numOverrides) |
Induces a phase change upon each amplitude of qureg, determined by a multi-variable exponential polynomial "phase function", and an explicit set of 'overriding' values at specific state indices. More... | |
| void | applyNamedPhaseFunc (Qureg qureg, int *qubits, int *numQubitsPerReg, int numRegs, enum bitEncoding encoding, enum phaseFunc functionNameCode) |
Induces a phase change upon each amplitude of qureg, determined by a named (and potentially multi-variable) phase function. More... | |
| void | applyNamedPhaseFuncOverrides (Qureg qureg, int *qubits, int *numQubitsPerReg, int numRegs, enum bitEncoding encoding, enum phaseFunc functionNameCode, long long int *overrideInds, qreal *overridePhases, int numOverrides) |
Induces a phase change upon each amplitude of qureg, determined by a named (and potentially multi-variable) phase function, and an explicit set of 'overriding' values at specific state indices. More... | |
| void | applyParamNamedPhaseFunc (Qureg qureg, int *qubits, int *numQubitsPerReg, int numRegs, enum bitEncoding encoding, enum phaseFunc functionNameCode, qreal *params, int numParams) |
Induces a phase change upon each amplitude of qureg, determined by a named, paramaterized (and potentially multi-variable) phase function. More... | |
| void | applyParamNamedPhaseFuncOverrides (Qureg qureg, int *qubits, int *numQubitsPerReg, int numRegs, enum bitEncoding encoding, enum phaseFunc functionNameCode, qreal *params, int numParams, long long int *overrideInds, qreal *overridePhases, int numOverrides) |
Induces a phase change upon each amplitude of qureg, determined by a named, parameterised (and potentially multi-variable) phase function, and an explicit set of 'overriding' values at specific state indices. More... | |
| void | applyPauliHamil (Qureg inQureg, PauliHamil hamil, Qureg outQureg) |
Modifies outQureg to be the result of applying PauliHamil (a Hermitian but not necessarily unitary operator) to inQureg. More... | |
| void | applyPauliSum (Qureg inQureg, enum pauliOpType *allPauliCodes, qreal *termCoeffs, int numSumTerms, Qureg outQureg) |
Modifies outQureg to be the result of applying the weighted sum of Pauli products (a Hermitian but not necessarily unitary operator) to inQureg. More... | |
| void | applyPhaseFunc (Qureg qureg, int *qubits, int numQubits, enum bitEncoding encoding, qreal *coeffs, qreal *exponents, int numTerms) |
Induces a phase change upon each amplitude of qureg, determined by the passed exponential polynomial "phase function". More... | |
| void | applyPhaseFuncOverrides (Qureg qureg, int *qubits, int numQubits, enum bitEncoding encoding, qreal *coeffs, qreal *exponents, int numTerms, long long int *overrideInds, qreal *overridePhases, int numOverrides) |
Induces a phase change upon each amplitude of qureg, determined by the passed exponential polynomial "phase function", and an explicit set of 'overriding' values at specific state indices. More... | |
| void | applyProjector (Qureg qureg, int qubit, int outcome) |
Force the target qubit of qureg into the given classical outcome, via a non-renormalising projection. More... | |
| void | applyQFT (Qureg qureg, int *qubits, int numQubits) |
Applies the quantum Fourier transform (QFT) to a specific subset of qubits of the register qureg. More... | |
| void | applyTrotterCircuit (Qureg qureg, PauliHamil hamil, qreal time, int order, int reps) |
Applies a trotterisation of unitary evolution 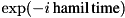 to to qureg. More... | |
Detailed Description
Non-physical operators which may be non-unitary, non-norm-preserving, even non-Hermitian.
Function Documentation
◆ applyDiagonalOp()
| void applyDiagonalOp | ( | Qureg | qureg, |
| DiagonalOp | op | ||
| ) |
Apply a diagonal operator, which is possibly non-unitary and non-Hermitian, to the entire qureg.
Let ![$d_j = \text{op.real}[j] + (\text{op.imag}[j])\,\text{i} $](form_36.png) , and
, and
![\[ \hat{D} = \begin{pmatrix} d_0 \\ & d_1 \\ & & \ddots \\ & & & d_{2^{\text{op.numQubits}}-1} \end{pmatrix}. \]](form_37.png)
If qureg is a state-vector 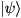 , this function performs
, this function performs 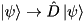 .
.
If qureg is a density-matrix 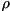 , this function performs
, this function performs 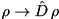 . Notice this has not applied
. Notice this has not applied 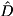 in the fashion of a unitary.
in the fashion of a unitary.
If your operator is unitary with unit amplitudes, the phases of which can be described by an analytic expression, you should instead use applyPhaseFunc() or applyNamedPhaseFunc() for significant memory and runtime savings.
- Parameters
-
[in,out] qureg the state to operate the diagonal operator upon [in] op the diagonal operator to apply
- Exceptions
-
invalidQuESTInputError() - if
opwas not created - if
opacts on a different number of qubits thanquregrepresents
- if
Definition at line 1127 of file QuEST.c.
References densmatr_applyDiagonalOp(), Qureg::isDensityMatrix, qasm_recordComment(), statevec_applyDiagonalOp(), and validateDiagonalOp().
Referenced by TEST_CASE().
◆ applyFullQFT()
| void applyFullQFT | ( | Qureg | qureg | ) |
Applies the quantum Fourier transform (QFT) to the entirety of qureg.
The effected unitary circuit (shown here for 4 qubits, bottom qubit is 0) resembles
![\[ \begin{tikzpicture}[scale=.5] \draw (-2, 5) -- (23, 5); \draw (-2, 3) -- (23, 3); \draw (-2, 1) -- (23, 1); \draw (-2, -1) -- (23, -1); \draw[fill=white] (-1, 4) -- (-1, 6) -- (1, 6) -- (1,4) -- cycle; \node[draw=none] at (0, 5) {H}; \draw(2, 5) -- (2, 3); \draw[fill=black] (2, 5) circle (.2); \draw[fill=black] (2, 3) circle (.2); \draw(4, 5) -- (4, 1); \draw[fill=black] (4, 5) circle (.2); \draw[fill=black] (4, 1) circle (.2); \draw(6, 5) -- (6, -1); \draw[fill=black] (6, 5) circle (.2); \draw[fill=black] (6, -1) circle (.2); \draw[fill=white] (-1+8, 4-2) -- (-1+8, 6-2) -- (1+8, 6-2) -- (1+8,4-2) -- cycle; \node[draw=none] at (8, 5-2) {H}; \draw(10, 5-2) -- (10, 3-2); \draw[fill=black] (10, 5-2) circle (.2); \draw[fill=black] (10, 3-2) circle (.2); \draw(12, 5-2) -- (12, 3-4); \draw[fill=black] (12, 5-2) circle (.2); \draw[fill=black] (12, 3-4) circle (.2); \draw[fill=white] (-1+8+6, 4-4) -- (-1+8+6, 6-4) -- (1+8+6, 6-4) -- (1+8+6,4-4) -- cycle; \node[draw=none] at (8+6, 5-4) {H}; \draw(16, 5-2-2) -- (16, 3-4); \draw[fill=black] (16, 5-2-2) circle (.2); \draw[fill=black] (16, 3-4) circle (.2); \draw[fill=white] (-1+8+6+4, 4-4-2) -- (-1+8+6+4, 6-4-2) -- (1+8+6+4, 6-4-2) -- (1+8+6+4,4-4-2) -- cycle; \node[draw=none] at (8+6+4, 5-4-2) {H}; \draw (20, 5) -- (20, -1); \draw (20 - .35, 5 + .35) -- (20 + .35, 5 - .35); \draw (20 - .35, 5 - .35) -- (20 + .35, 5 + .35); \draw (20 - .35, -1 + .35) -- (20 + .35, -1 - .35); \draw (20 - .35, -1 - .35) -- (20 + .35, -1 + .35); \draw (22, 3) -- (22, 1); \draw (22 - .35, 3 + .35) -- (22 + .35, 3 - .35); \draw (22 - .35, 3 - .35) -- (22 + .35, 3 + .35); \draw (22 - .35, 1 + .35) -- (22 + .35, 1 - .35); \draw (22 - .35, 1 - .35) -- (22 + .35, 1 + .35); \end{tikzpicture} \]](form_294.png)
though is performed more efficiently.
- If
quregis a state-vector, the output amplitudes are the discrete Fourier transform (DFT) of the input amplitudes, in the exact ordering. This is true even ifquregis unnormalised.
Precisely,![\[ \text{QFT} \, \left( \sum\limits_{x=0}^{2^N-1} \alpha_x |x\rangle \right) = \frac{1}{\sqrt{2^N}} \sum\limits_{x=0}^{2^N-1} \left( \sum\limits_{y=0}^{2^N-1} e^{2 \pi \, i \, x \, y / 2^N} \; \alpha_y \right) |x\rangle \]](form_295.png)
- If
quregis a density matrix , it will be changed under the unitary action of the QFT. This can be imagined as each mixed state-vector undergoing the DFT on its amplitudes. This is true even if
, it will be changed under the unitary action of the QFT. This can be imagined as each mixed state-vector undergoing the DFT on its amplitudes. This is true even if quregis unnormalised.![\[ \rho \; \rightarrow \; \text{QFT} \; \rho \; \text{QFT}^{\dagger} \]](form_296.png)
This function merges contiguous controlled-phase gates into single invocations of applyNamedPhaseFunc(), and hence is significantly faster than performing the QFT circuit directly.
Furthermore, in distributed mode, this function requires only
rounds of pair-wise communication, and hence is exponentially faster than directly performing the DFT on the amplitudes of
qureg.
- See also
- applyQFT() to apply the QFT to a sub-register of
qureg.
- applyQFT() to apply the QFT to a sub-register of
- Parameters
-
[in,out] qureg a state-vector or density matrix to modify
Definition at line 876 of file QuEST.c.
References agnostic_applyQFT(), Qureg::numQubitsRepresented, and qasm_recordComment().
Referenced by TEST_CASE().
◆ applyMatrix2()
| void applyMatrix2 | ( | Qureg | qureg, |
| int | targetQubit, | ||
| ComplexMatrix2 | u | ||
| ) |
Apply a general 2-by-2 matrix, which may be non-unitary.
The matrix is left-multiplied onto the state, for both state-vectors and density matrices.
Note this differs from the action of unitary() on a density matrix.
This function may leave qureg is an unnormalised state.
- See also
- Parameters
-
[in,out] qureg object representing the set of all qubits [in] targetQubit qubit to operate uupon[in] u matrix to apply
- Exceptions
-
invalidQuESTInputError() - if
targetQubitis outside [0,qureg.numQubitsRepresented)
- if
Definition at line 1084 of file QuEST.c.
References qasm_recordComment(), statevec_unitary(), and validateTarget().
Referenced by TEST_CASE().
◆ applyMatrix4()
| void applyMatrix4 | ( | Qureg | qureg, |
| int | targetQubit1, | ||
| int | targetQubit2, | ||
| ComplexMatrix4 | u | ||
| ) |
Apply a general 4-by-4 matrix, which may be non-unitary.
The matrix is left-multiplied onto the state, for both state-vectors and density matrices.
Note this differs from the action of twoQubitUnitary() on a density matrix.
targetQubit1 is treated as the least significant qubit in u, such that a row in u is dotted with the vector 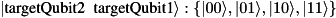
For example,
will invoke multiplication
![\[ \begin{pmatrix} u_{00} & u_{01} & u_{02} & u_{03} \\ u_{10} & u_{11} & u_{12} & u_{13} \\ u_{20} & u_{21} & u_{22} & u_{23} \\ u_{30} & u_{31} & u_{32} & u_{33} \end{pmatrix} \begin{pmatrix} |ba\rangle = |00\rangle \\ |ba\rangle = |01\rangle \\ |ba\rangle = |10\rangle \\ |ba\rangle = |11\rangle \end{pmatrix} \]](form_212.png)
This function may leave qureg is an unnormalised state.
Note that in distributed mode, this routine requires that each node contains at least 4 amplitudes. This means an q-qubit register (state vector or density matrix) can be distributed by at most 2^q/4 nodes.
- See also
- Parameters
-
[in,out] qureg object representing the set of all qubits [in] targetQubit1 first qubit to operate on, treated as least significant in u[in] targetQubit2 second qubit to operate on, treated as most significant in u[in] u matrix to apply
- Exceptions
-
invalidQuESTInputError() - if
targetQubit1ortargetQubit2are outside [0,qureg.numQubitsRepresented) - if
targetQubit1equalstargetQubit2 - if each node cannot fit 4 amplitudes in distributed mode
- if
Definition at line 1093 of file QuEST.c.
References qasm_recordComment(), statevec_twoQubitUnitary(), validateMultiQubitMatrixFitsInNode(), and validateMultiTargets().
Referenced by TEST_CASE().
◆ applyMatrixN()
| void applyMatrixN | ( | Qureg | qureg, |
| int * | targs, | ||
| int | numTargs, | ||
| ComplexMatrixN | u | ||
| ) |
Apply a general N-by-N matrix, which may be non-unitary, on any number of target qubits.
The matrix is left-multiplied onto the state, for both state-vectors and density matrices. Note this differs from the action of multiQubitUnitary() on a density matrix.
The first target qubit in targs is treated as least significant in u. For example,
will invoke multiplication
![\[ \begin{pmatrix} u_{00} & u_{01} & u_{02} & u_{03} & u_{04} & u_{05} & u_{06} & u_{07} \\ u_{10} & u_{11} & u_{12} & u_{13} & u_{14} & u_{15} & u_{16} & u_{17} \\ u_{20} & u_{21} & u_{22} & u_{23} & u_{24} & u_{25} & u_{26} & u_{27} \\ u_{30} & u_{31} & u_{32} & u_{33} & u_{34} & u_{35} & u_{36} & u_{37} \\ u_{40} & u_{41} & u_{42} & u_{43} & u_{44} & u_{45} & u_{46} & u_{47} \\ u_{50} & u_{51} & u_{52} & u_{53} & u_{54} & u_{55} & u_{56} & u_{57} \\ u_{60} & u_{61} & u_{62} & u_{63} & u_{64} & u_{65} & u_{66} & u_{67} \\ u_{70} & u_{71} & u_{72} & u_{73} & u_{74} & u_{75} & u_{76} & u_{77} \\ \end{pmatrix} \begin{pmatrix} |cba\rangle = |000\rangle \\ |cba\rangle = |001\rangle \\ |cba\rangle = |010\rangle \\ |cba\rangle = |011\rangle \\ |cba\rangle = |100\rangle \\ |cba\rangle = |101\rangle \\ |cba\rangle = |110\rangle \\ |cba\rangle = |111\rangle \end{pmatrix} \]](form_217.png)
This function may leave qureg is an unnormalised state.
The passed ComplexMatrix must be a compatible size with the specified number of target qubits, otherwise an error is thrown.
Note that in multithreaded mode, each thread will clone 2^numTargs amplitudes, and store these in the runtime stack. Using t threads, the total memory overhead of this function is t*2^numTargs. For many targets (e.g. 16 qubits), this may cause a stack-overflow / seg-fault (e.g. on a 1 MiB stack).
Note too that in distributed mode, this routine requires that each node contains at least 2^numTargs amplitudes in the register. This means an q-qubit register (state vector or density matrix) can be distributed by at most 2^q / 2^numTargs nodes.
- See also
- Parameters
-
[in,out] qureg object representing the set of all qubits [in] targs a list of the target qubits, ordered least significant to most in u[in] numTargs the number of target qubits [in] u matrix to apply
- Exceptions
-
invalidQuESTInputError() - if any index in
targsis outside of [0,qureg.numQubitsRepresented) - if
targsare not unique - if
uis not of a compatible size withnumTargs - if a node cannot fit the required number of target amplitudes in distributed mode
- if any index in
Definition at line 1103 of file QuEST.c.
References qasm_recordComment(), statevec_multiQubitUnitary(), validateMultiQubitMatrix(), and validateMultiTargets().
Referenced by TEST_CASE().
◆ applyMultiControlledMatrixN()
| void applyMultiControlledMatrixN | ( | Qureg | qureg, |
| int * | ctrls, | ||
| int | numCtrls, | ||
| int * | targs, | ||
| int | numTargs, | ||
| ComplexMatrixN | u | ||
| ) |
Apply a general N-by-N matrix, which may be non-unitary, with additional controlled qubits.
The matrix is left-multiplied onto the state, for both state-vectors and density matrices. Hence, this function differs from multiControlledMultiQubitUnitary() by more than just permitting a non-unitary matrix.
This function may leave qureg is an unnormalised state.
Any number of control and target qubits can be specified. This effects the many-qubit matrix
![\[ \begin{pmatrix} 1 \\ & 1 \\\ & & \ddots \\ & & & u_{00} & u_{01} & \dots \\ & & & u_{10} & u_{11} & \dots \\ & & & \vdots & \vdots & \ddots \end{pmatrix} \]](form_221.png)
on the control and target qubits.
The target qubits in targs are treated as ordered least significant to most significant in u.
The passed ComplexMatrix must be a compatible size with the specified number of target qubits, otherwise an error is thrown.
Note that in multithreaded mode, each thread will clone 2^numTargs amplitudes, and store these in the runtime stack. Using t threads, the total memory overhead of this function is t*2^numTargs. For many targets (e.g. 16 qubits), this may cause a stack-overflow / seg-fault (e.g. on a 1 MiB stack).
Note that in distributed mode, this routine requires that each node contains at least 2^numTargs amplitudes. This means an q-qubit register (state vector or density matrix) can be distributed by at most 2^q / 2^numTargs nodes.
- Parameters
-
[in,out] qureg object representing the set of all qubits [in] ctrls a list of the control qubits [in] numCtrls the number of control qubits [in] targs a list of the target qubits, ordered least to most significant [in] numTargs the number of target qubits [in] u matrix to apply
- Exceptions
-
invalidQuESTInputError() - if any index in
ctrlsandtargsis outside of [0,qureg.numQubitsRepresented) - if
ctrlsandtargsare not unique - if matrix
uis not a compatible size withnumTargs - if a node cannot fit the required number of target amplitudes in distributed mode
- if any index in
Definition at line 1114 of file QuEST.c.
References getQubitBitMask(), qasm_recordComment(), statevec_multiControlledMultiQubitUnitary(), validateMultiControlsMultiTargets(), and validateMultiQubitMatrix().
Referenced by TEST_CASE().
◆ applyMultiVarPhaseFunc()
| void applyMultiVarPhaseFunc | ( | Qureg | qureg, |
| int * | qubits, | ||
| int * | numQubitsPerReg, | ||
| int | numRegs, | ||
| enum bitEncoding | encoding, | ||
| qreal * | coeffs, | ||
| qreal * | exponents, | ||
| int * | numTermsPerReg | ||
| ) |
Induces a phase change upon each amplitude of qureg, determined by a multi-variable exponential polynomial "phase function".
This is a multi-variable extension of applyPhaseFunc(), whereby multiple sub-registers inform separate variables in the exponential polynomial function, and effects a diagonal unitary operator.
Arguments
coeffs,exponentsandnumTermsPerRegtogether specify a real exponential polynomial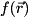 of the form
of the form ![\[ f(r_1, \; \dots, \; r_{\text{numRegs}}) = \sum\limits_j^{\text{numRegs}} \; \sum\limits_{i}^{\text{numTermsPerReg}[j]} \; c_{i,j} \; {r_j}^{\; p_{i,j}}\,, \]](form_263.png)
where both coefficients
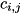 and exponents
and exponents 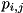 can be any real number, subject to constraints described below.
can be any real number, subject to constraints described below.
Whilecoeffsandexponentsare flat lists, they should be considered grouped into #numRegssublists with lengths given bynumTermsPerReg(which itself has lengthnumRegs).
For example,int numRegs = 3;qreal coeffs[] = {1, 2, 4, -3.14};qreal exponents[] = {2, 1, 5, 0.5 };int numTermsPerReg[] = {1, 2, 1 };constitutes the function
![\[ f(\vec{r}) = 1 \, {r_1}^2 + 2 \, {r_2} + 4 \, {r_2}^{5} - 3.14 \, {r_3}^{0.5}. \]](form_266.png)
This means lists
coeffsandexponentsshould both be of length equal to the sum ofnumTermsPerReg.Unlike applyPhaseFunc(), applyMultiVarPhaseFunc() places additional constraints on the exponents in
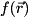 , due to the exponentially growing costs of overriding diverging indices. Namely:
, due to the exponentially growing costs of overriding diverging indices. Namely:
exponentsmust not contain a negative number, since this would result in a divergence when that register is zero, which would need to be overriden for every other register basis state. If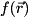 must contain a negative exponent, you should instead call applyPhaseFuncOverrides() once for each register/variable, and override the zero index for the relevant variable. This works, because
must contain a negative exponent, you should instead call applyPhaseFuncOverrides() once for each register/variable, and override the zero index for the relevant variable. This works, because ![\[ \exp( i \sum_j f_j(r_j) ) = \prod_j \exp(i f_j(r_j) ). \]](form_267.png)
exponentsmust not contain a fractional number ifendoding= TWOS_COMPLEMENT, because such a term would produce illegal complex values at negative register indices. Similar to the problem above, each negative register index would require overriding at every index of the other registers, and hence require an exponential number of overrides. Therefore, if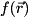 must contain a negative exponent, you should instead call applyPhaseFuncOverrides() once for each register/variable, and override every negative index of each register in turn.
must contain a negative exponent, you should instead call applyPhaseFuncOverrides() once for each register/variable, and override every negative index of each register in turn.
Lists
qubitsandnumQubitsPerRegtogether describe #numRegssub-registers ofqureg, which can each contain a different number of qubits.
Althoughqubitsis a flat list of unique qubit indices, it should be imagined grouped into #numRegssub-lists, of lengths given bynumQubitsPerReg.
For example,int qubits[] = {0,1, 3,4,5, 7}int numQubitsPerReg[] = {2, 3, 1};int numRegs = 3;describes three sub-registers, which are bolded below in an eight-qubit zero-state.
![\[ |r_3\rangle \; |0\rangle \; |r_2\rangle \; |0\rangle \; |r_1\rangle = |\mathbf{0}\rangle \; |0\rangle \; |\mathbf{000}\rangle \; |0\rangle \; |\mathbf{00}\rangle \]](form_268.png)
Note that the qubits need not be ordered increasing, and qubits within each sub-register are assumed ordered least to most significant in that sub-register.
List
qubitsshould have length equal to the sum of elements innumQubitsPerReg.- Each sub-register is associated with a variable
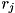 in phase function
in phase function 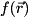 .
.
For a given computational basis state ofqureg, the value of each variable is determined by the binary value in the corresponding sub-register, when intepreted with bitEncodingencoding.
See bitEncoding for more information.
- The function
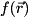 specifies the phase change to induce upon amplitude
specifies the phase change to induce upon amplitude 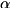 of computational basis state with the nominated sub-registers encoding values
of computational basis state with the nominated sub-registers encoding values 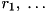 .
.
For example, using the sub-registers in the previous example and![\[ \alpha \, |r_{\text{numRegs}}, \; \dots, \; r_2, \; r_1 \rangle \rightarrow \, \exp(i f(\vec{r}\,)) \; \alpha \, |r_{\text{numRegs}}, \; \dots, \; r_2, \; r_1 \rangle. \]](form_271.png)
encoding=UNSIGNED, the following states receive amplitude factors:![\[ \begin{aligned} |\mathbf{0}\rangle \; |0\rangle \; |\mathbf{000}\rangle \; |0\rangle \; |\mathbf{00}\rangle & \rightarrow \, e^{i f(r_3=0,r_2=0,r_1=0)} \\ |\mathbf{0}\rangle \; |0\rangle \; |\mathbf{000}\rangle \; |0\rangle \; |\mathbf{01}\rangle & \rightarrow \, e^{i f(r_3=0,r_2=0,r_1=1)} \\ |\mathbf{0}\rangle \; |0\rangle \; |\mathbf{000}\rangle \; |0\rangle \; |\mathbf{10}\rangle & \rightarrow \, e^{i f(r_3=0,r_2=0,r_1=2)} \\ |\mathbf{0}\rangle \; |0\rangle \; |\mathbf{000}\rangle \; |0\rangle \; |\mathbf{11}\rangle & \rightarrow \, e^{i f(r_3=0,r_2=0,r_1=3)} \\ |\mathbf{0}\rangle \; |0\rangle \; |\mathbf{000}\rangle \; |1\rangle \; |\mathbf{00}\rangle & \rightarrow \, e^{i f(r_3=0,r_2=0,r_1=0)} \\ & \;\;\;\vdots \\ |\mathbf{0}\rangle \; |0\rangle \; |\mathbf{111}\rangle \; |0\rangle \; |\mathbf{01}\rangle & \rightarrow \, e^{i f(r_3=0,r_2=7,r_1=1)} \\ & \;\;\;\vdots \\ |\mathbf{1}\rangle \; |0\rangle \; |\mathbf{111}\rangle \; |0\rangle \; |\mathbf{11}\rangle & \rightarrow \, e^{i f(r_3=1,r_2=7,r_1=3)} \end{aligned} \]](form_272.png)
- If
quregis a density matrix , then its elements are modified as
, then its elements are modified as
where![\[ \alpha \, |j\rangle\langle k| \; \rightarrow \; \exp(i \, (f(\vec{r}_j) - f(\vec{r}_k)) \, ) \; \alpha \, |j\rangle\langle k|, \]](form_273.png)
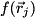 and
and 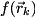 are determined as above.
are determined as above.
The interpreted phase function can be previewed in the QASM log, as a comment.
For example:would show, for the above example,
// Here, applyMultiVarPhaseFunc() multiplied a complex scalar of the form// exp(i (// + 1 x^2// + 2 y + 4 y^(-1)// - 3.14 z^0.5 ))// upon substates informed by qubits (under an unsigned binary encoding)// |x> = {0, 1}// |y> = {3, 4, 5}// |z> = {7}
- See also
- applyMultiVarPhaseFuncOverrides() to additionally specify explicit phases for specific sub-register values.
- applyNamedPhaseFunc() for a set of specific and potentially multi-variable phase functions.
- applyPhaseFunc() for a single-variable polynomial exponential phase function, which is approximately twice as fast.
- applyDiagonalOp() to apply a non-unitary diagonal Operators.
- Parameters
-
[in,out] qureg the state-vector or density matrix to be modified [in] qubits a list of all the qubit indices contained in each sub-register [in] numQubitsPerReg a list of the lengths of each sub-list in qubits[in] numRegs the number of sub-registers, which is the length of both numQubitsPerRegandnumTermsPerReg[in] encoding the bitEncoding under which to infer the binary value 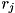 from the bits of a sub-register
from the bits of a sub-register [in] coeffs the coefficients of all terms of the exponential polynomial phase function 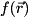
[in] exponents the exponents of all terms of the exponential polynomial phase function 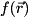
[in] numTermsPerReg a list of the number of coeffandexponentterms supplied for each variable/sub-register
- Exceptions
-
invalidQuESTInputError() - if any qubit in
qubitshas an invalid index (i.e. does not satisfy 0 <= qubit <qureg.numQubitsRepresented) - if the elements of
qubitsare not unique (including if sub-registers overlap) - if
numRegs<= 0 ornumRegs> 100 (constrained byMAX_NUM_REGS_APPLY_ARBITRARY_PHASEin QuEST_precision.h) - if
encodingis not a valid bitEncoding - if the size of any sub-register is incompatible with
encoding(e.g. contains fewer than two qubits inencoding=TWOS_COMPLEMENT) - if any element of
numTermsPerRegis < 1 - if
exponentscontains a negative number - if
exponentscontains a fractional number despiteencoding= TWOS_COMPLEMENT
- if any qubit in
Definition at line 761 of file QuEST.c.
References Qureg::isDensityMatrix, Qureg::numQubitsRepresented, qasm_recordMultiVarPhaseFunc(), shiftSubregIndices(), statevec_applyMultiVarPhaseFuncOverrides(), validateMultiRegBitEncoding(), validateMultiVarPhaseFuncTerms(), and validateQubitSubregs().
Referenced by TEST_CASE().
◆ applyMultiVarPhaseFuncOverrides()
| void applyMultiVarPhaseFuncOverrides | ( | Qureg | qureg, |
| int * | qubits, | ||
| int * | numQubitsPerReg, | ||
| int | numRegs, | ||
| enum bitEncoding | encoding, | ||
| qreal * | coeffs, | ||
| qreal * | exponents, | ||
| int * | numTermsPerReg, | ||
| long long int * | overrideInds, | ||
| qreal * | overridePhases, | ||
| int | numOverrides | ||
| ) |
Induces a phase change upon each amplitude of qureg, determined by a multi-variable exponential polynomial "phase function", and an explicit set of 'overriding' values at specific state indices.
See applyMultiVarPhaseFunc() first for a full description.
- As in applyMultiVarPhaseFunc(), the arguments
coeffsandexponentsspecify a multi-variable phase function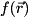 , where
, where 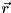 is determined by the sub-registers in
is determined by the sub-registers in qubits, and bitEncodingencodingfor each basis state ofqureg.
Additionally,
overrideIndsis a list of lengthnumOverrideswhich specifies the values of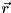 for which to explicitly set the induced phase change.
for which to explicitly set the induced phase change.
While flat,overrideIndsshould be imagined grouped into sub-lists of lengthnumRegs, which specify the full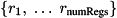 coordinate to override.
coordinate to override.
Each sublist corresponds to a single element ofoverridePhases.
For example,int numRegs = 3;int numOverrides = 2;long long int overrideInds[] = { 0,0,0, 1,2,3 };denotes that any basis state of
quregwith sub-register values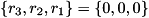 (or
(or 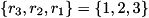 ) should receive phase change
) should receive phase change 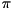 (or
(or 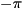 ) in lieu of
) in lieu of 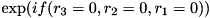 .
.
Note that you cannot use applyMultiVarPhaseFuncOverrides() to override divergences in
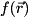 , since each diverging value
, since each diverging value 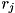 would need to be overriden as an
would need to be overriden as an 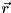 coordinate for every basis state of the other registers; the number of overrides grows exponentially. Ergo, if
coordinate for every basis state of the other registers; the number of overrides grows exponentially. Ergo, if exponentscontains a negative number (diverging at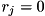 ), or
), or exponentscontains a fractional number despiteencoding= TWOS_COMPLEMENT (producing complex phases at negative indices), you must instead call applyPhaseFuncOverrides() for each variable in turn and override the diverging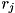 (each independently of the other registers).
(each independently of the other registers). The interpreted overrides can be previewed in the QASM log, as a comment.
For example:may show
// Here, applyMultiVarPhaseFunc() multiplied ...// though with overrides// |x=0, y=0, z=0> -> exp(i 3.14159)// |x=1, y=2, z=3> -> exp(i (-3.14159))
- See also
- applyNamedPhaseFunc() for a set of specific and potentially multi-variable phase functions.
- applyDiagonalOp() to apply a non-unitary diagonal Operators.
- Parameters
-
[in,out] qureg the state-vector or density-matrix to be modified [in] qubits a list of all the qubit indices contained in each sub-register [in] numQubitsPerReg a list of the lengths of each sub-list in qubits[in] numRegs the number of sub-registers, which is the length of both numQubitsPerRegandnumTermsPerReg[in] encoding the bitEncoding under which to infer the binary value 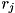 from the bits of a sub-register
from the bits of a sub-register [in] coeffs the coefficients of all terms of the exponential polynomial phase function 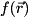
[in] exponents the exponents of all terms of the exponential polynomial phase function 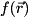
[in] numTermsPerReg a list of the number of coeffandexponentterms supplied for each variable/sub-register[in] overrideInds a flattened list of sub-register coordinates (values of 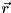 ) of which to explicit set the phase change
) of which to explicit set the phase change [in] overridePhases a list of replacement phase changes, for the corresponding 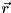 values in
values in overrideInds[in] numOverrides the lengths of list overridePhases(but not necessarily ofoverrideInds)
- Exceptions
-
invalidQuESTInputError() - if any qubit in
qubitshas an invalid index (i.e. does not satisfy 0 <= qubit <qureg.numQubitsRepresented) - if the elements of
qubitsare not unique (including if sub-registers overlap) - if
numRegs<= 0 ornumRegs> 100 (constrained byMAX_NUM_REGS_APPLY_ARBITRARY_PHASEin QuEST_precision.h) - if
encodingis not a valid bitEncoding - if the size of any sub-register is incompatible with
encoding(e.g. contains fewer than two qubits inencoding=TWOS_COMPLEMENT) - if any element of
numTermsPerRegis < 1 - if
exponentscontains a negative number - if
exponentscontains a fractional number despiteencoding= TWOS_COMPLEMENT - if any value in
overrideIndsis not producible by its corresponding sub-register under the givenencoding(e.g. 2 unsigned qubits cannot represent index 9) - if
numOverrides< 0
- if any qubit in
Definition at line 778 of file QuEST.c.
References Qureg::isDensityMatrix, Qureg::numQubitsRepresented, qasm_recordMultiVarPhaseFunc(), shiftSubregIndices(), statevec_applyMultiVarPhaseFuncOverrides(), validateMultiRegBitEncoding(), validateMultiVarPhaseFuncOverrides(), validateMultiVarPhaseFuncTerms(), and validateQubitSubregs().
Referenced by TEST_CASE().
◆ applyNamedPhaseFunc()
| void applyNamedPhaseFunc | ( | Qureg | qureg, |
| int * | qubits, | ||
| int * | numQubitsPerReg, | ||
| int | numRegs, | ||
| enum bitEncoding | encoding, | ||
| enum phaseFunc | functionNameCode | ||
| ) |
Induces a phase change upon each amplitude of qureg, determined by a named (and potentially multi-variable) phase function.
This effects a diagonal unitary operator, with a phase function 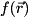 which may not be simply expressible as an exponential polynomial in functions applyPhaseFunc() and applyMultiVarPhaseFunc().
which may not be simply expressible as an exponential polynomial in functions applyPhaseFunc() and applyMultiVarPhaseFunc().
Arguments qubits and numQubitsPerReg encode sub-registers of qureg in the same manner as in applyMultiVarPhaseFunc():
Lists
qubitsandnumQubitsPerRegtogether describe #numRegssub-registers ofqureg, which can each contain a different number of qubits.
Althoughqubitsis a flat list of unique qubit indices, it should be imagined grouped into #numRegssub-lists, of lengths given bynumQubitsPerReg.
For example,int qubits[] = {0,1, 3,4,5, 7}int numQubitsPerReg[] = {2, 3, 1};int numRegs = 3;describes three sub-registers, which are bolded below in an eight-qubit zero-state.
![\[ |r_3\rangle \; |0\rangle \; |r_2\rangle \; |0\rangle \; |r_1\rangle = |\mathbf{0}\rangle \; |0\rangle \; |\mathbf{000}\rangle \; |0\rangle \; |\mathbf{00}\rangle \]](form_268.png)
Note that the qubits need not be ordered increasing, and qubits within each sub-register are assumed ordered least to most significant in that sub-register.
List
qubitsshould have length equal to the sum of elements innumQubitsPerReg.- Each sub-register is associated with a variable
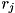 in phase function
in phase function 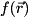 .
.
For a given computational basis state ofqureg, the value of each variable is determined by the binary value in the corresponding sub-register, when intepreted with bitEncodingencoding.
See bitEncoding for more information.
Argument
functionNameCodedetermines the phase function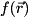 .
.
For example,describes phase function
![\[ f(\vec{r}) = \sqrt{ {r_1}^2 + {r_2}^2 + {r_3} ^2 }. \]](form_283.png)
See phaseFunc for a list and description of all named phase functions.
Some phase functions, likeSCALED_NORM, require passing additional parameters, through the function applyParamNamedPhaseFunc().
If the phase function
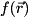 diverges at one or more
diverges at one or more 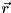 values, you should instead use applyNamedPhaseFuncOverrides() and specify explicit phase changes for these coordinates. Otherwise, the corresponding amplitudes of
values, you should instead use applyNamedPhaseFuncOverrides() and specify explicit phase changes for these coordinates. Otherwise, the corresponding amplitudes of quregwill become indeterminate (likeNaN).
- The function
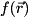 specifies the phase change to induce upon amplitude
specifies the phase change to induce upon amplitude 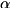 of computational basis state with the nominated sub-registers encoding values
of computational basis state with the nominated sub-registers encoding values 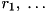 .
.
For example, using the sub-registers in the above example and![\[ \alpha \, |r_{\text{numRegs}}, \; \dots, \; r_2, \; r_1 \rangle \rightarrow \, \exp(i f(\vec{r}\,)) \; \alpha \, |r_{\text{numRegs}}, \; \dots, \; r_2, \; r_1 \rangle. \]](form_271.png)
encoding=UNSIGNED, the following states receive amplitude factors:![\[ \begin{aligned} |\mathbf{0}\rangle \; |0\rangle \; |\mathbf{000}\rangle \; |0\rangle \; |\mathbf{00}\rangle & \rightarrow \, e^{i f(r_3=0,r_2=0,r_1=0)} \\ |\mathbf{0}\rangle \; |0\rangle \; |\mathbf{000}\rangle \; |0\rangle \; |\mathbf{01}\rangle & \rightarrow \, e^{i f(r_3=0,r_2=0,r_1=1)} \\ |\mathbf{0}\rangle \; |0\rangle \; |\mathbf{000}\rangle \; |0\rangle \; |\mathbf{10}\rangle & \rightarrow \, e^{i f(r_3=0,r_2=0,r_1=2)} \\ |\mathbf{0}\rangle \; |0\rangle \; |\mathbf{000}\rangle \; |0\rangle \; |\mathbf{11}\rangle & \rightarrow \, e^{i f(r_3=0,r_2=0,r_1=3)} \\ |\mathbf{0}\rangle \; |0\rangle \; |\mathbf{000}\rangle \; |1\rangle \; |\mathbf{00}\rangle & \rightarrow \, e^{i f(r_3=0,r_2=0,r_1=0)} \\ & \;\;\;\vdots \\ |\mathbf{0}\rangle \; |0\rangle \; |\mathbf{111}\rangle \; |0\rangle \; |\mathbf{01}\rangle & \rightarrow \, e^{i f(r_3=0,r_2=7,r_1=1)} \\ & \;\;\;\vdots \\ |\mathbf{1}\rangle \; |0\rangle \; |\mathbf{111}\rangle \; |0\rangle \; |\mathbf{11}\rangle & \rightarrow \, e^{i f(r_3=1,r_2=7,r_1=3)} \end{aligned} \]](form_272.png)
- If
quregis a density matrix, its elements are modified to
where![\[ \alpha \, |j\rangle\langle k| \; \rightarrow \; \exp(i (f(\vec{r}_j) \, - \, f(\vec{r}_k))) \; \alpha \, |j\rangle\langle k| \]](form_284.png)
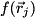 and
and 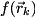 are determined as above. This is equivalent to modification
are determined as above. This is equivalent to modification
where![\[ \rho \; \rightarrow \; \hat{D} \, \rho \, \hat{D}^\dagger \]](form_285.png)
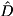 is the diagonal unitary
is the diagonal unitary ![\[ \hat{D} = \text{diag}\, \{ \; e^{i f(\vec{r_0})}, \; e^{i f(\vec{r_1})}, \; \dots \; \}. \]](form_286.png)
The interpreted phase function can be previewed in the QASM log, as a comment.
For example:startRecordingQASM(qureg);applyNamedPhaseFunc(qureg, ..., INVERSE_DISTANCE, ... );printRecordedQASM(qureg);may show
// Here, applyNamedPhaseFunc() multiplied a complex scalar of form// exp(i 1 / sqrt((x-y)^2 + (z-t)^2))
- See also
- applyNamedPhaseFuncOverrides() to additionally specify phase values for specific sub-register indices.
- applyParamNamedPhaseFunc() to specify named phase functions which require additional parameters.
- applyPhaseFunc() to specify a general single-variable exponential polynomial phase function.
- applyMultiVarPhaseFunc() to specify a general multi-variable exponential polynomial phase function.
- applyDiagonalOp() to apply a non-unitary diagonal Operators.
- Parameters
-
[in,out] qureg the state-vector or density-matrix to be modified [in] qubits a list of all the qubit indices contained in each sub-register [in] numQubitsPerReg a list of the lengths of each sub-list in qubits[in] numRegs the number of sub-registers, which is the length of both numQubitsPerRegandnumTermsPerReg[in] encoding the bitEncoding under which to infer the binary value 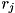 from the bits of a sub-register
from the bits of a sub-register [in] functionNameCode the phaseFunc 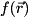
- Exceptions
-
invalidQuESTInputError() - if any qubit in
qubitshas an invalid index (i.e. does not satisfy 0 <= qubit <qureg.numQubitsRepresented) - if the elements of
qubitsare not unique (including if sub-registers overlap) - if
numRegs<= 0 ornumRegs> 100 (constrained byMAX_NUM_REGS_APPLY_ARBITRARY_PHASEin QuEST_precision.h) - if
encodingis not a valid bitEncoding - if the size of any sub-register is incompatible with
encoding(e.g. contains fewer than two qubits inencoding=TWOS_COMPLEMENT) - if
functionNameCodeis not a valid phaseFunc - if
functionNameCoderequires additional parameters, which must instead be passed with applyParamNamedPhaseFunc()
- if any qubit in
Definition at line 796 of file QuEST.c.
References Qureg::isDensityMatrix, Qureg::numQubitsRepresented, qasm_recordNamedPhaseFunc(), shiftSubregIndices(), statevec_applyParamNamedPhaseFuncOverrides(), validateMultiRegBitEncoding(), validatePhaseFuncName(), and validateQubitSubregs().
Referenced by TEST_CASE().
◆ applyNamedPhaseFuncOverrides()
| void applyNamedPhaseFuncOverrides | ( | Qureg | qureg, |
| int * | qubits, | ||
| int * | numQubitsPerReg, | ||
| int | numRegs, | ||
| enum bitEncoding | encoding, | ||
| enum phaseFunc | functionNameCode, | ||
| long long int * | overrideInds, | ||
| qreal * | overridePhases, | ||
| int | numOverrides | ||
| ) |
Induces a phase change upon each amplitude of qureg, determined by a named (and potentially multi-variable) phase function, and an explicit set of 'overriding' values at specific state indices.
See applyNamedPhaseFunc() first for a full description.
- As in applyNamedPhaseFunc(),
functionNameCodespecifies a multi-variable phase function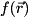 , where
, where 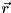 is determined by the sub-registers in
is determined by the sub-registers in qubits, and bitEncodingencodingfor each basis state ofqureg.
Additionally,
overrideIndsis a list of lengthnumOverrideswhich specifies the values of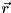 for which to explicitly set the induced phase change.
for which to explicitly set the induced phase change.
While flat,overrideIndsshould be imagined grouped into sub-lists of lengthnumRegs, which specify the full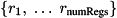 coordinate to override.
coordinate to override.
Each sublist corresponds to a single element ofoverridePhases.
For example,int numRegs = 3;int numOverrides = 2;long long int overrideInds[] = { 0,0,0, 1,2,3 };denotes that any basis state of
quregwith sub-register values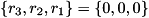 (or
(or 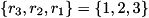 ) should receive phase change
) should receive phase change 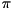 (or
(or 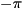 ) in lieu of
) in lieu of 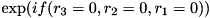 .
.
The interpreted overrides can be previewed in the QASM log, as a comment.
For example:may show
// Here, applyNamedPhaseFunc() multiplied ...// though with overrides// |x=0, y=0, z=0> -> exp(i 3.14159)// |x=1, y=2, z=3> -> exp(i (-3.14159))
- See also
- applyParamNamedPhaseFuncOverrides() to specify parameterised named phase functions, with phase overrides.
- applyPhaseFunc() to specify a general single-variable exponential polynomial phase function.
- applyMultiVarPhaseFunc() to specify a general multi-variable exponential polynomial phase function.
- applyDiagonalOp() to apply a non-unitary diagonal Operators.
- Parameters
-
[in,out] qureg the state-vector pr density-matrix to be modified [in] qubits a list of all the qubit indices contained in each sub-register [in] numQubitsPerReg a list of the lengths of each sub-list in qubits[in] numRegs the number of sub-registers, which is the length of both numQubitsPerRegandnumTermsPerReg[in] encoding the bitEncoding under which to infer the binary value 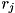 from the bits of a sub-register
from the bits of a sub-register [in] functionNameCode the phaseFunc 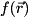
[in] overrideInds a flattened list of sub-register coordinates (values of 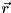 ) of which to explicit set the phase change
) of which to explicit set the phase change [in] overridePhases a list of replacement phase changes, for the corresponding 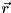 values in
values in overrideInds[in] numOverrides the lengths of list overridePhases(but not necessarily ofoverrideInds)
- Exceptions
-
invalidQuESTInputError() - if any qubit in
qubitshas an invalid index (i.e. does not satisfy 0 <= qubit <qureg.numQubitsRepresented) - if the elements of
qubitsare not unique (including if sub-registers overlap) - if
numRegs<= 0 ornumRegs> 100 (constrained byMAX_NUM_REGS_APPLY_ARBITRARY_PHASEin QuEST_precision.h) - if
encodingis not a valid bitEncoding - if the size of any sub-register is incompatible with
encoding(e.g. contains fewer than two qubits inencoding=TWOS_COMPLEMENT) - if
functionNameCodeis not a valid phaseFunc - if
functionNameCoderequires additional parameters, which must instead be passed with applyParamNamedPhaseFunc() - if any value in
overrideIndsis not producible by its corresponding sub-register under the givenencoding(e.g. 2 unsigned qubits cannot represent index 9) - if
numOverrides< 0
- if any qubit in
Definition at line 813 of file QuEST.c.
References Qureg::isDensityMatrix, Qureg::numQubitsRepresented, qasm_recordNamedPhaseFunc(), shiftSubregIndices(), statevec_applyParamNamedPhaseFuncOverrides(), validateMultiRegBitEncoding(), validateMultiVarPhaseFuncOverrides(), validatePhaseFuncName(), and validateQubitSubregs().
Referenced by TEST_CASE().
◆ applyParamNamedPhaseFunc()
| void applyParamNamedPhaseFunc | ( | Qureg | qureg, |
| int * | qubits, | ||
| int * | numQubitsPerReg, | ||
| int | numRegs, | ||
| enum bitEncoding | encoding, | ||
| enum phaseFunc | functionNameCode, | ||
| qreal * | params, | ||
| int | numParams | ||
| ) |
Induces a phase change upon each amplitude of qureg, determined by a named, paramaterized (and potentially multi-variable) phase function.
See applyNamedPhaseFunc() for full documentation.
This function merely accepts additional phaseFunc names which accept one (or more) parameters.
Argument
functionNameCode, which determines the phase function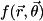 , can include parameterised phaseFunc names like
, can include parameterised phaseFunc names like SCALED_NORM, which require additional parameters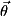 passed via list
passed via list params.
For example,qreal params[] = {0.5};int numParams = 1;applyParamNamedPhaseFunc(..., functionNameCode, params, numParams);invokes phase function
![\[ f(\vec{r}, \theta)|_{\theta=0.5} \; = \; 0.5 \prod_j^{\text{numRegs}} \; r_j\,. \]](form_289.png)
See phaseFunc for all named phased functions.
Functions with divergences, like
INVERSE_NORMandSCALED_INVERSE_DISTANCE, must accompany an extra parameter to specify an overriding phase at the divergence. For example,int numParams = 2;applyParamNamedPhaseFunc(..., functionNameCode, params, numParams);invokes phase function
![\[ f(\vec{r}, \theta)|_{\theta=0.5} \; = \; \begin{cases} \pi & \;\;\; \vec{r}=\vec{0} \\ \displaystyle 0.5 \left[ \sum_j^{\text{numRegs}} {r_j}^2 \right]^{-1/2} & \;\;\;\text{otherwise} \end{cases}. \]](form_290.png)
Notice the order of the parameters matches the order of the words in the
phaseFunc.Functions
SCALED_INVERSE_SHIFTED_NORMandSCALED_INVERSE_SHIFTED_DISTANCE, which can have denominators arbitrarily close to zero, will invoke the divergence parameter whenever the denominator is smaller than (or equal to) machine precisionREAL_EPS.Functions allowing the shifting of sub-register values, which are
SCALED_INVERSE_SHIFTED_NORMandSCALED_INVERSE_SHIFTED_DISTANCE, need these shift values to be passed in theparamsargument after the scaling and divergence override parameters listed above. The functionSCALED_INVERSE_SHIFTED_NORMneeds as many extra parameters, as there are sub-registers;SCALED_INVERSE_SHIFTED_DISTANCEneeds one extra parameter for each pair of sub-registers. For example,int qubits[] = {0,1,2,3, 4,5,6,7};int qubitsPerReg[] = {4, 4};int numParams = 4;applyParamNamedPhaseFunc(..., qubits, qubitsPerReg, 2, ..., functionNameCode, params, numParams);invokes phase function
![\[ f(\vec{r}) \; = \; \begin{cases} \pi & \;\;\; \vec{r}=\vec{0} \\ \displaystyle 0.5 \left[(r_1-0.8)^2 + (r_2+0.3)^2\right]^{-1/2} & \;\;\;\text{otherwise} \end{cases}. \]](form_291.png)
and
int qubits[] = {0,1, 2,3, 4,5, 6,7};int qubitsPerReg[] = {2, 2, 2, 2};int numParams = 4;applyParamNamedPhaseFunc(..., qubits, qubitsPerReg, 4, ..., functionNameCode, params, numParams);invokes phase function
![\[ f(\vec{r}) \; = \; \begin{cases} \pi & \;\;\; \vec{r}=\vec{0} \\ \displaystyle 0.5 \left[(r_1-r_2-0.8)^2 + (r_3-r_4+0.3)^2\right]^{-1/2} & \;\;\;\text{otherwise} \end{cases}. \]](form_292.png)
You can further override
at one or more
values via applyParamNamedPhaseFuncOverrides().
The interpreted parameterised phase function can be previewed in the QASM log, as a comment.
For example:may show
// Here, applyNamedPhaseFunc() multiplied a complex scalar of form// exp(i (-0.5) / (x y z))
- See also
- applyParamNamedPhaseFuncOverrides() to additionally specify phase values for specific sub-register indices.
- applyPhaseFunc() to specify a general single-variable exponential polynomial phase function.
- applyMultiVarPhaseFunc() to specify a general multi-variable exponential polynomial phase function.
- applyDiagonalOp() to apply a non-unitary diagonal Operators.
- Parameters
-
[in,out] qureg the state-vector or density-matrix to be modified [in] qubits a list of all the qubit indices contained in each sub-register [in] numQubitsPerReg a list of the lengths of each sub-list in qubits[in] numRegs the number of sub-registers, which is the length of both numQubitsPerRegandnumTermsPerReg[in] encoding the bitEncoding under which to infer the binary value 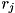 from the bits of a sub-register
from the bits of a sub-register [in] functionNameCode the phaseFunc 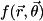
[in] params a list of any additional parameters needed by the phaseFunc functionNameCode[in] numParams the length of list params
- Exceptions
-
invalidQuESTInputError() - if any qubit in
qubitshas an invalid index (i.e. does not satisfy 0 <= qubit <qureg.numQubitsRepresented) - if the elements of
qubitsare not unique (including if sub-registers overlap) - if
numRegs<= 0 ornumRegs> 100 (constrained byMAX_NUM_REGS_APPLY_ARBITRARY_PHASEin QuEST_precision.h) - if
encodingis not a valid bitEncoding - if the size of any sub-register is incompatible with
encoding(e.g. contains fewer than two qubits inencoding=TWOS_COMPLEMENT) - if
functionNameCodeis not a valid phaseFunc - if
numParamsis incompatible withfunctionNameCode(for example, no parameters were passed toSCALED_PRODUCT)
- if any qubit in
Definition at line 831 of file QuEST.c.
References Qureg::isDensityMatrix, Qureg::numQubitsRepresented, qasm_recordNamedPhaseFunc(), shiftSubregIndices(), statevec_applyParamNamedPhaseFuncOverrides(), validateMultiRegBitEncoding(), validatePhaseFuncName(), and validateQubitSubregs().
Referenced by TEST_CASE().
◆ applyParamNamedPhaseFuncOverrides()
| void applyParamNamedPhaseFuncOverrides | ( | Qureg | qureg, |
| int * | qubits, | ||
| int * | numQubitsPerReg, | ||
| int | numRegs, | ||
| enum bitEncoding | encoding, | ||
| enum phaseFunc | functionNameCode, | ||
| qreal * | params, | ||
| int | numParams, | ||
| long long int * | overrideInds, | ||
| qreal * | overridePhases, | ||
| int | numOverrides | ||
| ) |
Induces a phase change upon each amplitude of qureg, determined by a named, parameterised (and potentially multi-variable) phase function, and an explicit set of 'overriding' values at specific state indices.
See applyParamNamedPhaseFunc() and applyNamedPhaseFunc() first for a full description.
- As in applyParamNamedPhaseFunc(),
functionNameCodespecifies a parameterised multi-variable phase function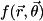 , where
, where 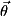 is passed in list
is passed in list params, and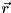 is determined both by the sub-registers in
is determined both by the sub-registers in qubits, and bitEncodingencodingfor each basis state ofqureg.
Additionally,
overrideIndsis a list of lengthnumOverrideswhich specifies the values of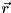 for which to explicitly set the induced phase change.
for which to explicitly set the induced phase change.
While flat,overrideIndsshould be imagined grouped into sub-lists of lengthnumRegs, which specify the full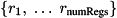 coordinate to override.
coordinate to override.
Each sublist corresponds to a single element ofoverridePhases.
For example,int numRegs = 3;int numOverrides = 2;long long int overrideInds[] = { 0,0,0, 1,2,3 };denotes that any basis state of
quregwith sub-register values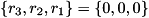 (or
(or 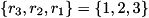 ) should receive phase change
) should receive phase change 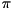 (or
(or 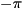 ) in lieu of
) in lieu of 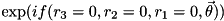 .
.
The interpreted overrides can be previewed in the QASM log, as a comment.
For example:may show
// Here, applyParamNamedPhaseFunc() multiplied ...// though with overrides// |x=0, y=0, z=0> -> exp(i 3.14159)// |x=1, y=2, z=3> -> exp(i (-3.14159))
- See also
- applyPhaseFunc() to specify a general single-variable exponential polynomial phase function.
- applyMultiVarPhaseFunc() to specify a general multi-variable exponential polynomial phase function.
- applyDiagonalOp() to apply a non-unitary diagonal Operators.
- Parameters
-
[in,out] qureg the state-vector or density-matrix to be modified [in] qubits a list of all the qubit indices contained in each sub-register [in] numQubitsPerReg a list of the lengths of each sub-list in qubits[in] numRegs the number of sub-registers, which is the length of both numQubitsPerRegandnumTermsPerReg[in] encoding the bitEncoding under which to infer the binary value 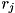 from the bits of a sub-register
from the bits of a sub-register [in] functionNameCode the phaseFunc 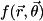
[in] params a list of any additional parameters 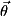 needed by the phaseFunc
needed by the phaseFunc functionNameCode[in] numParams the length of list params[in] overrideInds a flattened list of sub-register coordinates (values of 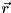 ) of which to explicit set the phase change
) of which to explicit set the phase change [in] overridePhases a list of replacement phase changes, for the corresponding 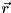 values in
values in overrideInds[in] numOverrides the lengths of list overridePhases(but not necessarily ofoverrideInds)
- Exceptions
-
invalidQuESTInputError() - if any qubit in
qubitshas an invalid index (i.e. does not satisfy 0 <= qubit <qureg.numQubitsRepresented) - if the elements of
qubitsare not unique (including if sub-registers overlap) - if
numRegs<= 0 ornumRegs> 100 (constrained byMAX_NUM_REGS_APPLY_ARBITRARY_PHASEin QuEST_precision.h) - if
encodingis not a valid bitEncoding - if the size of any sub-register is incompatible with
encoding(e.g. contains fewer than two qubits inencoding=TWOS_COMPLEMENT) - if
functionNameCodeis not a valid phaseFunc - if
numParamsis incompatible withfunctionNameCode(for example, no parameters were passed toSCALED_PRODUCT) - if any value in
overrideIndsis not producible by its corresponding sub-register under the givenencoding(e.g. 2 unsigned qubits cannot represent index 9) - if
numOverrides< 0
- if any qubit in
Definition at line 848 of file QuEST.c.
References Qureg::isDensityMatrix, Qureg::numQubitsRepresented, qasm_recordNamedPhaseFunc(), shiftSubregIndices(), statevec_applyParamNamedPhaseFuncOverrides(), validateMultiRegBitEncoding(), validateMultiVarPhaseFuncOverrides(), validatePhaseFuncName(), and validateQubitSubregs().
Referenced by TEST_CASE().
◆ applyPauliHamil()
| void applyPauliHamil | ( | Qureg | inQureg, |
| PauliHamil | hamil, | ||
| Qureg | outQureg | ||
| ) |
Modifies outQureg to be the result of applying PauliHamil (a Hermitian but not necessarily unitary operator) to inQureg.
Note that afterward, outQureg may no longer be normalised and ergo not a state-vector or density matrix. Users must therefore be careful passing outQureg to other QuEST functions which assume normalisation in order to function correctly.
This is merely an encapsulation of applyPauliSum(), which can refer to for elaborated doc.
Letting hamil be expressed as 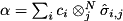 (where
(where 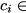
hamil.termCoeffs and 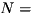
hamil.numQubits), this function effects 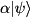 on state-vector
on state-vector 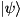 and
and 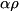 (left matrix multiplication) on density matrix
(left matrix multiplication) on density matrix 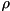 .
.
In theory, inQureg is unchanged though its state is temporarily modified and is reverted by re-applying Paulis (XX=YY=ZZ=I), so may see a change by small numerical errors. The initial state in outQureg is not used.
inQureg and outQureg must both be state-vectors, or both density matrices, of equal dimensions to hamil. inQureg cannot be outQureg.
This function works by applying each Pauli product in hamil to inQureg in turn, and adding the resulting state (weighted by a coefficient in termCoeffs) to the initially-blanked outQureg. Ergo it should scale with the total number of Pauli operators specified (excluding identities), and the qureg dimension.
- Parameters
-
[in] inQureg the register containing the state which outQuregwill be set to, under the action ofhamil.inQuregshould be unchanged, though may vary slightly due to numerical error.[in] hamil a weighted sum of products of pauli operators [out] outQureg the qureg to modify to be the result of applyling hamilto the state ininQureg
- Exceptions
-
invalidQuESTInputError() - if any code in
hamil.pauliCodesis not a valid Pauli code - if
numSumTerms<= 0 - if
inQuregis not of the same type and dimensions asoutQuregandhamil
- if any code in
Definition at line 1059 of file QuEST.c.
References PauliHamil::numSumTerms, PauliHamil::pauliCodes, qasm_recordComment(), statevec_applyPauliSum(), PauliHamil::termCoeffs, validateMatchingQuregDims(), validateMatchingQuregPauliHamilDims(), validateMatchingQuregTypes(), and validatePauliHamil().
Referenced by TEST_CASE().
◆ applyPauliSum()
| void applyPauliSum | ( | Qureg | inQureg, |
| enum pauliOpType * | allPauliCodes, | ||
| qreal * | termCoeffs, | ||
| int | numSumTerms, | ||
| Qureg | outQureg | ||
| ) |
Modifies outQureg to be the result of applying the weighted sum of Pauli products (a Hermitian but not necessarily unitary operator) to inQureg.
Note that afterward, outQureg may no longer be normalised and ergo not a state-vector or density matrix. Users must therefore be careful passing outQureg to other QuEST functions which assume normalisation in order to function correctly.
Letting 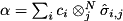 be the operators indicated by
be the operators indicated by allPauliCodes (where 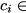
termCoeffs and 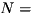
qureg.numQubitsRepresented), this function effects 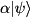 on state-vector
on state-vector 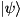 and
and 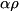 (left matrix multiplication) on density matrix
(left matrix multiplication) on density matrix 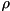 .
.
allPauliCodes is an array of length numSumTerms* specifies which Pauli operators to apply, where 0 = qureg.numQubitsRepresented whichPAULI_I, 1 = PAULI_X, 2 = PAULI_Y, 3 = PAULI_Z. For each sum term, a Pauli operator must be specified for EVERY qubit in qureg; each set of numSumTerms operators will be grouped into a product. termCoeffs is an arrray of length numSumTerms containing the term coefficients. For example, on a 3-qubit state-vector,
will apply Hermitian operation 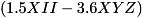 (where in this notation, the left-most operator applies to the least-significant qubit, i.e. that with index 0).
(where in this notation, the left-most operator applies to the least-significant qubit, i.e. that with index 0).
In theory, inQureg is unchanged though its state is temporarily modified and is reverted by re-applying Paulis (XX=YY=ZZ=I), so may see a change by small numerical errors. The initial state in outQureg is not used.
inQureg and outQureg must both be state-vectors, or both density matrices, of equal dimensions. inQureg cannot be outQureg.
This function works by applying each Pauli product to inQureg in turn, and adding the resulting state (weighted by a coefficient in termCoeffs) to the initially-blanked outQureg. Ergo it should scale with the total number of Pauli operators specified (excluding identities), and the qureg dimension.
- See also
- Parameters
-
[in] inQureg the register containing the state which outQuregwill be set to, under the action of the Hermitiain operator specified by the Pauli codes.inQuregshould be unchanged, though may vary slightly due to numerical error.[in] allPauliCodes a list of the Pauli codes (0=PAULI_I, 1=PAULI_X, 2=PAULI_Y, 3=PAULI_Z) of all Paulis involved in the products of terms. A Pauli must be specified for each qubit in the register, in every term of the sum. [in] termCoeffs The coefficients of each term in the sum of Pauli products [in] numSumTerms The total number of Pauli products specified [out] outQureg the qureg to modify to be the result of applyling the weighted Pauli sum operator to the state in inQureg
- Exceptions
-
invalidQuESTInputError() - if any code in
allPauliCodesis not in {0,1,2,3} - if numSumTerms <= 0
- if
inQuregis not of the same type and dimensions asoutQureg
- if any code in
Definition at line 1048 of file QuEST.c.
References Qureg::numQubitsRepresented, qasm_recordComment(), statevec_applyPauliSum(), validateMatchingQuregDims(), validateMatchingQuregTypes(), validateNumPauliSumTerms(), and validatePauliCodes().
Referenced by TEST_CASE().
◆ applyPhaseFunc()
| void applyPhaseFunc | ( | Qureg | qureg, |
| int * | qubits, | ||
| int | numQubits, | ||
| enum bitEncoding | encoding, | ||
| qreal * | coeffs, | ||
| qreal * | exponents, | ||
| int | numTerms | ||
| ) |
Induces a phase change upon each amplitude of qureg, determined by the passed exponential polynomial "phase function".
This effects a diagonal unitary of unit complex scalars, targeting the nominated qubits.
Arguments
coeffsandexponentstogether specify a real exponential polynomial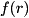 with
with numTermsterms, of the form![\[ f(r) = \sum\limits_{i}^{\text{numTerms}} \text{coeffs}[i] \; r^{\, \text{exponents}[i]}\,, \]](form_246.png)
where both
coeffsandexponentscan be negative, positive and fractional. For example,constitutes the function
![\[ f(r) = 1 \, r^2 - 3.14 \, r^{-5.5}. \]](form_247.png)
Note you cannot use fractional exponents with
encoding= TWOS_COMPLEMENT, since the negative indices would generate (illegal) complex phases, and must be overriden with applyPhaseFuncOverrides().
If your function
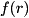 diverges at one or more
diverges at one or more 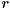 values, you must instead use applyPhaseFuncOverrides() and specify explicit phase changes for these values. Otherwise, the corresponding amplitudes of the state-vector will become indeterminate (like
values, you must instead use applyPhaseFuncOverrides() and specify explicit phase changes for these values. Otherwise, the corresponding amplitudes of the state-vector will become indeterminate (like NaN). Note that use of any negative exponent will result in divergences at .
. - The function
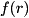 specifies the phase change to induce upon amplitude
specifies the phase change to induce upon amplitude 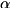 of computational basis state with index
of computational basis state with index 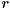 , such that
, such that
The index![\[ \alpha \, |r\rangle \rightarrow \, \exp(i f(r)) \; \alpha \, |r\rangle. \]](form_250.png)
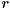 associated with each computational basis state is determined by the binary value of the specified
associated with each computational basis state is determined by the binary value of the specified qubits(ordered least to most significant), interpreted under the given bitEncodingencoding.
For example, underencoding=UNSIGNEDandqubits= {0,1},![\[ \begin{aligned} |0\mathbf{00}\rangle & \rightarrow \, e^{i f(0)}\,|0\mathbf{00}\rangle \\ |0\mathbf{01}\rangle & \rightarrow \, e^{i f(1)}\,|0\mathbf{01}\rangle \\ |0\mathbf{10}\rangle & \rightarrow \, e^{i f(2)}\,|0\mathbf{10}\rangle \\ |0\mathbf{11}\rangle & \rightarrow \, e^{i f(3)}\,|0\mathbf{11}\rangle \\ |1\mathbf{00}\rangle & \rightarrow \, e^{i f(0)}\,|1\mathbf{00}\rangle \\ |1\mathbf{01}\rangle & \rightarrow \, e^{i f(1)}\,|1\mathbf{01}\rangle \\ |1\mathbf{10}\rangle & \rightarrow \, e^{i f(2)}\,|1\mathbf{10}\rangle \\ |1\mathbf{11}\rangle & \rightarrow \, e^{i f(3)}\,|1\mathbf{11}\rangle \end{aligned} \]](form_251.png)
- If
quregis a density matrix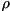 , this function modifies
, this function modifies quregto
where![\[ \rho \rightarrow \hat{D} \, \rho \, \hat{D}^\dagger \]](form_252.png)
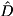 is the diagonal unitary operator
is the diagonal unitary operator
This means element![\[ \hat{D} = \text{diag} \, \{ \; e^{i f(r_0)}, \; e^{i f(r_1)}, \; \dots \; \}. \]](form_253.png)
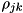 is modified to
is modified to ![\[ \alpha \, |j\rangle\langle k| \; \rightarrow \; e^{i (f(r_j) - f(r_k))} \; \alpha \, |j\rangle\langle k| \]](form_255.png)
The interpreted phase function can be previewed in the QASM log, as a comment.
For example:may show
// Here, applyPhaseFunc() multiplied a complex scalar of the form// exp(i (1 x^3))// upon every substate |x>, informed by qubits (under an unsigned binary encoding)// {4, 1, 2, 0}
This function may become numerically imprecise for quickly growing phase functions which admit very large phases, for example of 10^10.
- See also
- applyPhaseFuncOverrides() to override the phase function for specific states.
- applyMultiVarPhaseFunc() for multi-variable exponential polynomial phase functions.
- applyNamedPhaseFunc() for a set of specific phase functions.
- applyDiagonalOp() to apply a non-unitary diagonal Operators.
- Parameters
-
[in,out] qureg the state-vector or density matrix to be modified [in] qubits a list of the indices of the qubits which will inform 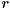 for each amplitude in
for each amplitude in qureg[in] numQubits the length of list qubits[in] encoding the bitEncoding under which to infer the binary value 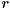 from the bits of
from the bits of qubitsin each basis state ofqureg[in] coeffs the coefficients of the exponential polynomial phase function 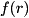
[in] exponents the exponents of the exponential polynomial phase function 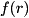
[in] numTerms the length of list coeffs, which must be the same as that ofexponents
- Exceptions
-
invalidQuESTInputError() - if any qubit in
qubitshas an invalid index (i.e. does not satisfy 0 <= qubit <qureg.numQubitsRepresented) - if the elements of
qubitsare not unique - if
numQubits< 0 ornumQubits>=qureg.numQubitsRepresented - if
encodingis not a valid bitEncoding - if
encodingis not compatible withnumQubits(e.g.TWOS_COMPLEMENTwith only 1 qubit) - if
exponentscontains a fractional number despiteencoding= TWOS_COMPLEMENT (you must instead use applyPhaseFuncOverrides() and override all negative indices) - if
exponentscontains a negative power (you must instead use applyPhaseFuncOverrides() and override the zero index) - if
numTerms<= 0
- if any qubit in
Definition at line 726 of file QuEST.c.
References Qureg::isDensityMatrix, Qureg::numQubitsRepresented, qasm_recordPhaseFunc(), shiftIndices(), statevec_applyPhaseFuncOverrides(), validateBitEncoding(), validateMultiQubits(), and validatePhaseFuncTerms().
Referenced by TEST_CASE().
◆ applyPhaseFuncOverrides()
| void applyPhaseFuncOverrides | ( | Qureg | qureg, |
| int * | qubits, | ||
| int | numQubits, | ||
| enum bitEncoding | encoding, | ||
| qreal * | coeffs, | ||
| qreal * | exponents, | ||
| int | numTerms, | ||
| long long int * | overrideInds, | ||
| qreal * | overridePhases, | ||
| int | numOverrides | ||
| ) |
Induces a phase change upon each amplitude of qureg, determined by the passed exponential polynomial "phase function", and an explicit set of 'overriding' values at specific state indices.
See applyPhaseFunc() first for a full description.
- As in applyPhaseFunc(), the arguments
coeffsandexponentsspecify a phase function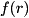 , where
, where 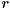 is determined by
is determined by qubitsandencodingfor each basis state ofqureg.
Additionally,
overrideIndsis a list of lengthnumOverrideswhich specifies the values of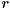 for which to explicitly set the induced phase change.
for which to explicitly set the induced phase change.
The overriding phase changes are specified in the corresponding elements ofoverridePhases.
For example,would effect the same diagonal unitary of applyPhaseFunc(), except that all instance of
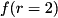 are overriden with phase
are overriden with phase 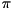 .
.
I.e.![\[ \begin{aligned} |0\mathbf{00}\rangle & \rightarrow \, e^{i f(0)}\,|0\mathbf{00}\rangle \\ |0\mathbf{01}\rangle & \rightarrow \, e^{i f(1)}\,|0\mathbf{01}\rangle \\ |0\mathbf{10}\rangle & \rightarrow \, e^{i \pi} \hspace{12pt} |0\mathbf{10}\rangle \\ |0\mathbf{11}\rangle & \rightarrow \, e^{i f(3)}\,|0\mathbf{11}\rangle \\ |1\mathbf{00}\rangle & \rightarrow \, e^{i f(0)}\,|1\mathbf{00}\rangle \\ |1\mathbf{01}\rangle & \rightarrow \, e^{i f(1)}\,|1\mathbf{01}\rangle \\ |1\mathbf{10}\rangle & \rightarrow \, e^{i \pi} \hspace{12pt} |1\mathbf{10}\rangle \\ |1\mathbf{11}\rangle & \rightarrow \, e^{i f(3)}\,|1\mathbf{11}\rangle \end{aligned} \]](form_257.png)
Note that if
encoding= TWOS_COMPLEMENT, and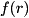 features a fractional exponent, then every negative phase index must be overriden. This is checked and enforced by QuEST's validation, unless there are more than 16 targeted qubits, in which case valid input is assumed (due to an otherwise prohibitive performance overhead).
features a fractional exponent, then every negative phase index must be overriden. This is checked and enforced by QuEST's validation, unless there are more than 16 targeted qubits, in which case valid input is assumed (due to an otherwise prohibitive performance overhead).
Overriding phases are checked at each computational basis state of
quregbefore evaluating the phase function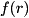 , and hence are useful for avoiding singularities or errors at diverging values of
, and hence are useful for avoiding singularities or errors at diverging values of 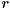 .
. - If
quregis a density matrix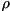 , the overrides determine the diagonal unitary matrix
, the overrides determine the diagonal unitary matrix 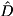 , which is then applied to
, which is then applied to quregas
This means that with overrides![\[ \rho \; \rightarrow \; \hat{D} \, \rho \hat{D}^\dagger. \]](form_258.png)
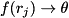 and
and 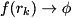 , element
, element 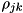 is modified to
is modified to ![\[ \alpha \, |j\rangle\langle k| \; \rightarrow \; \exp(\, i \, (\theta - \phi) \, ) \; \alpha \, |j\rangle\langle k|. \]](form_261.png)
The interpreted phase function and list of overrides can be previewed in the QASM log, as a comment.
For example:may show
// Here, applyPhaseFunc() multiplied a complex scalar of the form// exp(i (0.3 x^(-5) + 4 x^1 + 1 x^3))// upon every substate |x>, informed by qubits (under a two's complement binary encoding)// {4, 1, 2, 0}// though with overrides// |0> -> exp(i 3.14159)// |1> -> exp(i (-3.14159))// |2> -> exp(i 0)
- See also
- applyPhaseFunc() for full doc on how
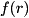 is evaluated.
is evaluated. - applyMultiVarPhaseFunc() for multi-variable exponential polynomial phase functions.
- applyNamedPhaseFunc() for a set of specific phase functions.
- applyDiagonalOp() to apply a non-unitary diagonal Operators.
- applyPhaseFunc() for full doc on how
- Parameters
-
[in,out] qureg the state-vector or density matrix to be modified [in] qubits a list of the indices of the qubits which will inform 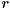 for each amplitude in
for each amplitude in qureg[in] numQubits the length of list qubits[in] encoding the bitEncoding under which to infer the binary value 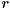 from the bits of
from the bits of qubitsin each basis state ofqureg[in] coeffs the coefficients of the exponential polynomial phase function 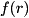
[in] exponents the exponents of the exponential polynomial phase function 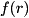
[in] numTerms the length of list coeffs, which must be the same as that ofexponents[in] overrideInds a list of sub-state indices (values of 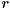 ) of which to explicit set the phase change
) of which to explicit set the phase change [in] overridePhases a list of replacement phase changes, for the corresponding 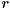 values in
values in overrideInds(one to one)[in] numOverrides the lengths of lists overrideIndsandoverridePhases
- Exceptions
-
invalidQuESTInputError() - if any qubit in
qubitshas an invalid index (i.e. does not satisfy 0 <= qubit <qureg.numQubitsRepresented) - if the elements of
qubitsare not unique - if
numQubits< 0 ornumQubits>=qureg.numQubitsRepresented - if
encodingis not a valid bitEncoding - if
encodingis not compatible withnumQubits(i.e.TWOS_COMPLEMENTwith 1 qubit) - if
numTerms<= 0 - if any value in
overrideIndsis not producible byqubitsunder the givenencoding(e.g. 2 unsigned qubits cannot represent index 9) - if
numOverrides< 0 - if
exponentscontains a negative power and the (consequently diverging) zero index is not contained inoverrideInds - if
encodingis TWOS_COMPLEMENT, andexponentscontains a fractional number, butoverrideIndsdoes not contain every possible negative index (checked only up to 16 targeted qubits)
- if any qubit in
Definition at line 743 of file QuEST.c.
References Qureg::isDensityMatrix, Qureg::numQubitsRepresented, qasm_recordPhaseFunc(), shiftIndices(), statevec_applyPhaseFuncOverrides(), validateBitEncoding(), validateMultiQubits(), validatePhaseFuncOverrides(), and validatePhaseFuncTerms().
Referenced by TEST_CASE().
◆ applyProjector()
| void applyProjector | ( | Qureg | qureg, |
| int | qubit, | ||
| int | outcome | ||
| ) |
Force the target qubit of qureg into the given classical outcome, via a non-renormalising projection.
This function zeroes all amplitudes in the state-vector or density-matrix which correspond to the opposite outcome given. Unlike collapseToOutcome(), it does not thereafter normalise qureg, and hence may leave it in a non-physical state.
Note there is no requirement that the outcome state has a non-zero proability, and hence this function may leave qureg in a blank state, like that produced by initBlankState().
- See also
- collapseToOutcome() for a norm-preserving equivalent, like a forced measurement
- Parameters
-
[in,out] qureg a state-vector or density matrix to modify [in] qubit the qubit to which to apply the projector [in] the single-qubit outcome ( 0or1) to projectqubitinto
- Exceptions
-
invalidQuESTInputError() - if
qubitis outside [0,qureg.numQubitsRepresented) - if
outcomeis not in {0,1}
- if
Definition at line 888 of file QuEST.c.
References densmatr_collapseToKnownProbOutcome(), Qureg::isDensityMatrix, qasm_recordComment(), qreal, statevec_collapseToKnownProbOutcome(), validateOutcome(), and validateTarget().
Referenced by TEST_CASE().
◆ applyQFT()
| void applyQFT | ( | Qureg | qureg, |
| int * | qubits, | ||
| int | numQubits | ||
| ) |
Applies the quantum Fourier transform (QFT) to a specific subset of qubits of the register qureg.
The order of qubits affects the ultimate unitary. The canonical full-state QFT (applyFullQFT()) is achieved by targeting every qubit in increasing order.
The effected unitary circuit (shown here for numQubits = 4) resembles
![\[ \begin{tikzpicture}[scale=.5] \draw (-2, 5) -- (23, 5); \node[draw=none] at (-4,5) {qubits[3]}; \draw (-2, 3) -- (23, 3); \node[draw=none] at (-4,3) {qubits[2]}; \draw (-2, 1) -- (23, 1); \node[draw=none] at (-4,1) {qubits[1]}; \draw (-2, -1) -- (23, -1); \node[draw=none] at (-4,-1) {qubits[0]}; \draw[fill=white] (-1, 4) -- (-1, 6) -- (1, 6) -- (1,4) -- cycle; \node[draw=none] at (0, 5) {H}; \draw(2, 5) -- (2, 3); \draw[fill=black] (2, 5) circle (.2); \draw[fill=black] (2, 3) circle (.2); \draw(4, 5) -- (4, 1); \draw[fill=black] (4, 5) circle (.2); \draw[fill=black] (4, 1) circle (.2); \draw(6, 5) -- (6, -1); \draw[fill=black] (6, 5) circle (.2); \draw[fill=black] (6, -1) circle (.2); \draw[fill=white] (-1+8, 4-2) -- (-1+8, 6-2) -- (1+8, 6-2) -- (1+8,4-2) -- cycle; \node[draw=none] at (8, 5-2) {H}; \draw(10, 5-2) -- (10, 3-2); \draw[fill=black] (10, 5-2) circle (.2); \draw[fill=black] (10, 3-2) circle (.2); \draw(12, 5-2) -- (12, 3-4); \draw[fill=black] (12, 5-2) circle (.2); \draw[fill=black] (12, 3-4) circle (.2); \draw[fill=white] (-1+8+6, 4-4) -- (-1+8+6, 6-4) -- (1+8+6, 6-4) -- (1+8+6,4-4) -- cycle; \node[draw=none] at (8+6, 5-4) {H}; \draw(16, 5-2-2) -- (16, 3-4); \draw[fill=black] (16, 5-2-2) circle (.2); \draw[fill=black] (16, 3-4) circle (.2); \draw[fill=white] (-1+8+6+4, 4-4-2) -- (-1+8+6+4, 6-4-2) -- (1+8+6+4, 6-4-2) -- (1+8+6+4,4-4-2) -- cycle; \node[draw=none] at (8+6+4, 5-4-2) {H}; \draw (20, 5) -- (20, -1); \draw (20 - .35, 5 + .35) -- (20 + .35, 5 - .35); \draw (20 - .35, 5 - .35) -- (20 + .35, 5 + .35); \draw (20 - .35, -1 + .35) -- (20 + .35, -1 - .35); \draw (20 - .35, -1 - .35) -- (20 + .35, -1 + .35); \draw (22, 3) -- (22, 1); \draw (22 - .35, 3 + .35) -- (22 + .35, 3 - .35); \draw (22 - .35, 3 - .35) -- (22 + .35, 3 + .35); \draw (22 - .35, 1 + .35) -- (22 + .35, 1 - .35); \draw (22 - .35, 1 - .35) -- (22 + .35, 1 + .35); \end{tikzpicture} \]](form_298.png)
though is performed more efficiently.
- If
quregis a state-vector, the output amplitudes are a kronecker product of the discrete Fourier transform (DFT) acting upon the targeted amplitudes, and the remaining.
Precisely,- let
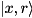 represent a computational basis state where
represent a computational basis state where 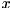 is the binary value of the targeted qubits, and
is the binary value of the targeted qubits, and 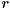 is the binary value of the remaining qubits.
is the binary value of the remaining qubits. - let
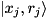 be the
be the 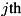 such state.
such state. - let
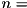
numQubits, and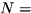
qureg.numQubitsRepresented.
Then, this function effects![\[ (\text{QFT}\otimes 1) \, \left( \sum\limits_{j=0}^{2^N-1} \alpha_j \, |x_j,r_j\rangle \right) = \frac{1}{\sqrt{2^n}} \sum\limits_{j=0}^{2^N-1} \alpha_j \left( \sum\limits_{y=0}^{2^n-1} e^{2 \pi \, i \, x_j \, y / 2^n} \; |y,r_j \rangle \right) \]](form_305.png)
- let
- If
quregis a density matrix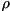 , it will be changed under the unitary action of the QFT. This can be imagined as each mixed state-vector undergoing the DFT on its amplitudes. This is true even if
, it will be changed under the unitary action of the QFT. This can be imagined as each mixed state-vector undergoing the DFT on its amplitudes. This is true even if quregis unnormalised.![\[ \rho \; \rightarrow \; \text{QFT} \; \rho \; \text{QFT}^{\dagger} \]](form_296.png)
This function merges contiguous controlled-phase gates into single invocations of applyNamedPhaseFunc(), and hence is significantly faster than performing the QFT circuit directly.
Furthermore, in distributed mode, this function requires only
rounds of pair-wise communication, and hence is exponentially faster than directly performing the DFT on the amplitudes of
qureg.
- See also
- applyFullQFT() to apply the QFT to the entirety of
qureg.
- applyFullQFT() to apply the QFT to the entirety of
- Parameters
-
[in,out] qureg a state-vector or density matrix to modify [in] qubits a list of the qubits to operate the QFT upon [in] numQubits the length of list qubits
- Exceptions
-
invalidQuESTInputError() - if any qubit in
qubitsis invalid, i.e. outside [0,qureg.numQubitsRepresented) - if
qubitscontain any repetitions - if
numQubits< 1 - if
numQubits>qureg.numQubitsRepresented
segmentation-fault - if
qubitscontains fewer elements thannumQubits
- if any qubit in
Definition at line 866 of file QuEST.c.
References agnostic_applyQFT(), qasm_recordComment(), and validateMultiTargets().
Referenced by TEST_CASE().
◆ applyTrotterCircuit()
| void applyTrotterCircuit | ( | Qureg | qureg, |
| PauliHamil | hamil, | ||
| qreal | time, | ||
| int | order, | ||
| int | reps | ||
| ) |
Applies a trotterisation of unitary evolution 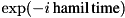 to
to qureg.
This is a sequence of unitary operators, effected by multiRotatePauli(), which together approximate the action of full unitary-time evolution under the given Hamiltonian.
Notate 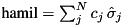 where
where  is a real coefficient in
is a real coefficient in hamil,  is the corresponding product of Pauli operators, of which there are a total
is the corresponding product of Pauli operators, of which there are a total  . Then,
. Then, order=1 performs first-order Trotterisation, whereby
![\[ \exp(-i \, \text{hamil} \, \text{time}) \approx \prod\limits^{\text{reps}} \prod\limits_{j=1}^{N} \exp(-i \, c_j \, \text{time} \, \hat\sigma_j / \text{reps}) \]](form_239.png)
order=2 performs the lowest order "symmetrized" Suzuki decomposition, whereby
![\[ \exp(-i \, \text{hamil} \, \text{time}) \approx \prod\limits^{\text{reps}} \left[ \prod\limits_{j=1}^{N} \exp(-i \, c_j \, \text{time} \, \hat\sigma_j / (2 \, \text{reps})) \prod\limits_{j=N}^{1} \exp(-i \, c_j \, \text{time} \, \hat\sigma_j / (2 \, \text{reps})) \right] \]](form_240.png)
Greater even values of order specify higher-order symmetrized decompositions ![$ S[\text{time}, \text{order}, \text{reps}] $](form_241.png) which satisfy
which satisfy
![\[ S[\text{time}, \text{order}, 1] = \left( \prod\limits^2 S[p \, \text{time}, \text{order}-2, 1] \right) S[ (1-4p)\,\text{time}, \text{order}-2, 1] \left( \prod\limits^2 S[p \, \text{time}, \text{order}-2, 1] \right) \]](form_242.png)
and
![\[ S[\text{time}, \text{order}, \text{reps}] = \prod\limits^{\text{reps}} S[\text{time}/\text{reps}, \text{order}, 1] \]](form_243.png)
where 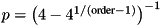 .
.
These formulations are taken from 'Finding Exponential Product Formulas of Higher Orders', Naomichi Hatano and Masuo Suzuki (2005) (arXiv).
Note that the applied Trotter circuit is captured by QASM, if QASM logging is enabled on qureg.
For example:
may show
- See also
- Parameters
-
[in,out] qureg the register to modify under the approximate unitary-time evolution [in] hamil the hamiltonian under which to approxiamte unitary-time evolution [in] time the target evolution time, which is permitted to be both positive and negative. [in] order the order of Trotter-Suzuki decomposition to use. Higher orders (necessarily even) are more accurate but prescribe an exponentially increasing number of gates. [in] reps the number of repetitions of the decomposition of the given order. This improves the accuracy but prescribes a linearly increasing number of gates.
- Exceptions
-
invalidQuESTInputError() - if
qureg.numQubitsRepresented!=hamil.numQubits - if
hamilcontains invalid parameters or Pauli codes, - if
orderis not in {1, 2, 4, 6, ...} - or if
reps<= 0
- if
Definition at line 1070 of file QuEST.c.
References agnostic_applyTrotterCircuit(), qasm_recordComment(), validateMatchingQuregPauliHamilDims(), validatePauliHamil(), and validateTrotterParams().
Referenced by TEST_CASE().