angle-sc
| Crates.io | angle-sc |
| lib.rs | angle-sc |
| version | 1.1.4 |
| created_at | 2024-02-11 09:54:51.212766+00 |
| updated_at | 2025-08-26 09:38:57.055665+00 |
| description | A Rust library for performing accurate and efficient trigonometry calculations. |
| homepage | https://github.com/kenba/angle-sc-rs |
| repository | https://github.com/kenba/angle-sc-rs |
| max_upload_size | |
| id | 1135749 |
| size | 103,478 |
documentation
README
angle-sc
A Rust library for performing accurate and efficient trigonometry calculations.
Description
The standard trigonometry functions: sin, cos, tan, etc.
give unexpected results for well-known angles.
This is due to floating-point round-off errors
and the functions taking parameters in radians instead of degrees.
The conversion from degrees to radians (and vice-versa) suffers from round-off error
because radians is based on the irrational number π.
This library uses the remquo
function to provide a sincos function to calculate more
accurate values than the standard sin and cos functions for angles in radians
and a sincosd function to calculate more accurate values
for angles in degrees.
The library also provides an Angle struct which represents an angle by its sine and cosine as the coordinates of a unit circle, see Figure 1.
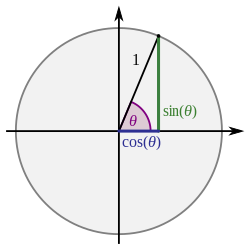 Figure 1 Unit circle formed by cos θ and sin θ
Figure 1 Unit circle formed by cos θ and sin θ
The Angle struct enables more accurate calculations of angle rotations and
conversions to and from degrees or radians.
Features
Degrees,RadiansandAngletypes;- functions for accurately calculating sines and cosines of angles in
DegreesorRadiansusing remquo; - functions for accurately calculating sines and cosines of differences of angles in
DegreesorRadiansusing the 2Sum algorithm; - functions for accurately calculating sums and differences of
Anglesusing trigonometric identities; - and some spherical trigonometry functions.
- The library is declared no_std.
Examples
The following example shows the round-off error inherent in calculating angles in radians.
It calculates the correct sine and cosine for 60° and converts them back
precisely to 60°, but it fails to convert them to the precise angle in radians: π/3.
use angle_sc::{Angle, Degrees, Radians, is_within_tolerance, trig};
let angle_60 = Angle::from(Degrees(60.0));
assert_eq!(trig::COS_30_DEGREES, angle_60.sin().0);
assert_eq!(0.5, angle_60.cos().0);
assert_eq!(60.0, Degrees::from(angle_60).0);
// assert_eq!(core::f64::consts::FRAC_PI_3, Radians::from(angle_60).0); // Fails because PI is irrational
assert!(is_within_tolerance(
core::f64::consts::FRAC_PI_3,
Radians::from(angle_60).0,
f64::EPSILON
));
The following example calculates the sine and cosine between the difference
of two angles in degrees: -155° - 175°.
It is more accurate than calling the Angle From trait in the example above
with the difference in degrees.
It is particularly useful for implementing the
Haversine formula
which requires sines and cosines of both longitude and latitude differences.
Note: in this example sine and cosine of 30° are converted precisely to π/6.
use angle_sc::{Angle, Degrees, Radians, trig};
// Difference of Degrees(-155.0) - Degrees(175.0)
let angle_30 = Angle::from((Degrees(-155.0), Degrees(175.0)));
assert_eq!(0.5, angle_30.sin().0);
assert_eq!(trig::COS_30_DEGREES, angle_30.cos().0);
assert_eq!(30.0, Degrees::from(angle_30).0);
assert_eq!(core::f64::consts::FRAC_PI_6, Radians::from(angle_30).0);
Design
Trigonometry Functions
The trig module contains accurate and efficient trigonometry functions.
Angle
The Angle struct represents an angle by its sine and cosine instead of in
degrees or radians, see Figure 2.
Figure 2 Angle Class Diagram
This representation an angle makes functions such as
rotating an angle +/-90° around the unit circle or calculating the opposite angle;
simple, accurate and efficient since they just involve changing the signs
and/or positions of the sin and cos values.
Angle Add and Sub traits are implemented using
angle sum and difference
trigonometric identities,
while Angle double
and half methods use other
trigonometric identities.
The sin and cos fields of Angle are UnitNegRanges:,
a newtype
with values in the range -1.0 to +1.0 inclusive.
Contribution
If you want to contribute through code or documentation, the Contributing guide is the best place to start. If you have any questions, please feel free to ask. Just please abide by our Code of Conduct.
License
angle-rs is provided under a MIT license, see LICENSE.


