merkle-tree-bulletin-board
| Crates.io | merkle-tree-bulletin-board |
| lib.rs | merkle-tree-bulletin-board |
| version | 0.3.0 |
| created_at | 2021-08-11 13:49:13.938042+00 |
| updated_at | 2023-03-10 11:54:26.825053+00 |
| description | A public bulletin board based upon Merkle trees. |
| homepage | https://github.com/RightToAskOrg/bulletin-board |
| repository | https://github.com/RightToAskOrg/bulletin-board |
| max_upload_size | |
| id | 434769 |
| size | 710,900 |
documentation
README
Merkle tree Bulletin board library
This implements a verifiable bulletin board based upon a Merkle tree. It is included in a repository which also contains a demo web server using it and a mysql backend.
What does it do?
There is a common addage "trust, but verify." Unfortunately, it is often impossible to verify, so if you are on the other end of this addage you should "be trustworthy, but be verifiable." This is designed to help a trustworthy bulletin board be verifiable.
Specifically, it allows for the continuous additions of elements to the bulletin board. Periodically, the bulletin board publishes a hashcode that is a commitment to all the elements published to date. Everyone can call their friends and check that everyone is being told the same hash, as evidence that everyone is being shown the same bulletin board. Anyone can check that any specific entry is referenced by said hash, and it is also possible to download the entire board (or additions since the last published hash) and check that is compatible with the provided hash.
This gives everyone confidence that the bulletin board operator is actually trustworthy. Or they have worked out how to reverse SHA2, which is considered hard. For a comparable definition of hard to "achieving world peace, prosperity and universal love" is hard.
How is this different from just publishing a file of all the entries, and publishing a hash of said file?
That solves a very similar problem in a simpler manner, and is preferable except for a couple of advantages of this approach:
- The Merkle tree lets one check that their own contribution is in the tree without having to download the entire bulletin board, in fact in time and space logarithmic in the size of the bulletin board.
- The operator may choose to refuse to give details on part of the tree after publishing a hash, without harming the verification of the rest of the tree. This is essential to be able to support censorship of the board, which is a legal requirement in much (most? all?) of the world for many applications. Assume standard rant about how biased such laws tend to be against things that would embarrass the powers that be. The operator can't hide the fact that something has been censored. Furthermore if you happen to know what the thing that was censored was, you can prove that it was the thing that was censored. The only thing that censorship does is refuse to provide the text that went into computing that particular leaf hash.
API
Start from the BulletinBoard structure, which has extensive documentation.
There are also helper verifier functions for inclusion proofs, but you should write your own as the whole point is to not need to trust this!
Backend
The bulletin board needs to store its information somewhere. There are a variety of ways of doing this, abstracted into a Backend. You can pretty easily write your own, or there are a variety of backends available:
- BackendMemory : Store everything transiently in memory. Good for tests and API demos.
- BackendFlatfile : like BackendMemory, but with flatfile persistent storage. Good for prototyping, but not suitable for production. This is used for the demo web server.
- BackendJournal : A wrapper around some other Backend that adds persistent storage of the changes between publications. Useful for adding bulk download support to some other backend.
- BackendMysql : This is in the merkle-tree-bulletin-board-backend-mysql folder. An example (usable) backend for a mysql or mariadb database. This could easily be adapted to a different SQL database.
How it works
See Wikipedia or Google for the general theory.
Different problems have somewhat different details depending upon their specific requirements. For the bulletin board, we want the additions of items to be an ongoing process, with occasional publications not synchronized to the additions. In particular, we can't assume a power of two entries on the board. We also record the text of the items rather than just their hash.
There are three different types of node in the system:
- Leaves. Each entry on the bulletin board is a leaf. Hash is of
0|timestamp|entry - Branches. Each branch contains a left and right node, which may be a branch or a leaf.
Everything on the left side of a branch precedes chronologically everything on the right side of
a branch. Both sides of a branch will be perfect balanced binary trees of the same depth. Each leaf and
branch will have a maximum of 1 parent. Hash is of
1|left|right - Published roots. When a publication is done, a published root node is created which
contains the hash of the prior published root, if any, and all the currently parentless
leaves and branches, of which there will be O(log N) where N is the number of leaves.
Hash is of
2|timestamp|prior|elements concatenated
See comments in hash_history.rs for precise description of the hash definitions.
Each time an entry is added, a new leaf is created. This is appended to a pending list of trees. (a leaf is considered a tree of depth 0). If the last two entries in the pending list have the same depth, then a new branch is created from those two, and replaces them on the pending list. This is continued recursively until the last two entries in the pending list are different depth (or there is only one entry in the list). This list will never get longer than 1+log base 2 of N, where N is the number of leaves.
This pending list contains the list of leaves and branches that have no parents; a published root is really a list of these elements. This means publishing a root hash is a relatively minor operation, very similar to a git commit object.
Many Merkle tree implementations bunch all nodes together into one tree at the point of publication, and ensure that that tree is present in future published trees. This common approach has the advantage that a published root is simpler as it only has one item in it, so an inclusion proof for a prior published root is just an inclusion proof for that one item instead of several items. However that approach leads to unbalanced binary trees, and often poor performance and/or complexity for inclusion proofs for old entries with respect to new published roots. The approach used in this library guarantees simple log N size inclusion proofs.
Example
The following picture from the demo shows the status after submitting three entries, A, B, and C, and then publishing a root.
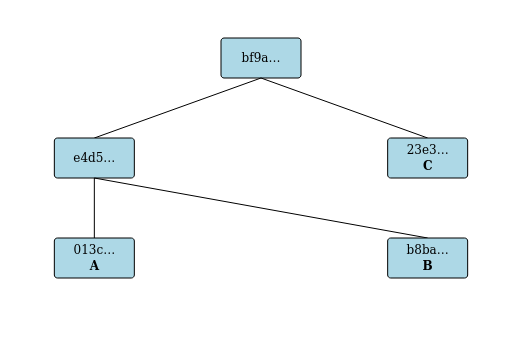
- The A produced a leaf with hash
013c... - The B produced a leaf with hash
b8ba... - A and B were then merged into a branch with hash
e4d5... - The C produced a leaf with hash
23e3... - Publication produced a published root with hash
bf9a...that referenced the branche4d5...and leaf23e3...
Then an extra entry "D" was submitted and a new publication was done.
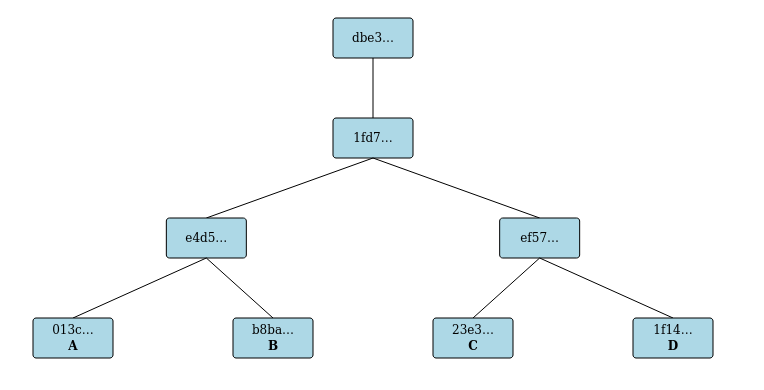
- The D produced a leaf with hash
1f14... - The C and D were merged into a branch with hash
ef57... - The AB and CD branches were merged into a branch with hash
1fd7... - Publication produced a published root with hash
dbe3...that referenced the branch1fd7...
Note that if you do the same with the demo you will get the same structure but different hash values as timestamps are included.
Note also that the picture above does not show (for space reasons) the link in the published root dbe3...
to the prior published root bf9a...
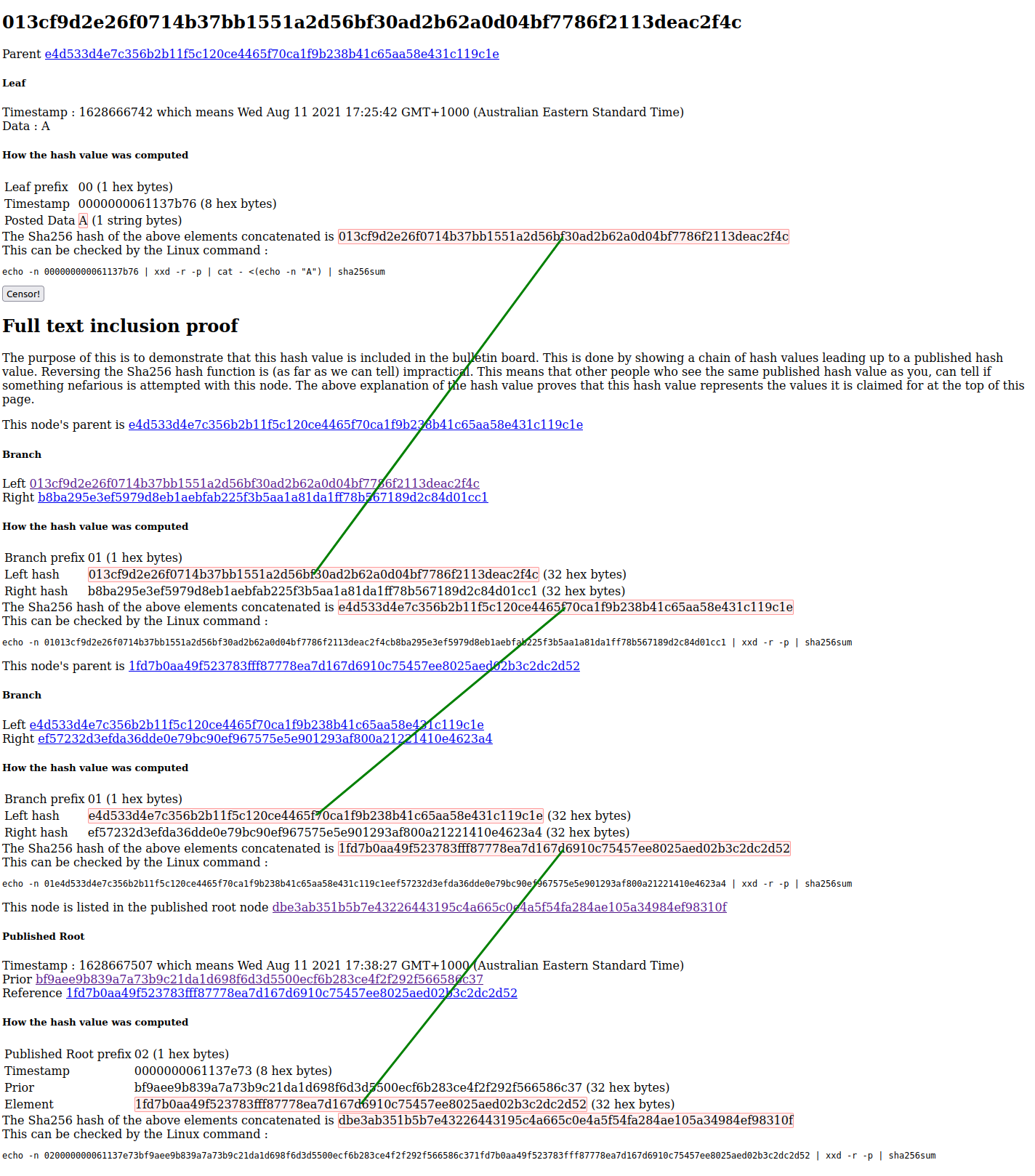
A full inclusion proof for the entry A in this example in the published root dbe3... is given
in the following screenshot of the demo webserver:
License
Copyright 2021 Thinking Cybersecurity Pty. Ltd.
Licensed under either of
- Apache License, Version 2.0 (LICENSE-APACHE or http://www.apache.org/licenses/LICENSE-2.0)
- MIT license (LICENSE-MIT or http://opensource.org/licenses/MIT)
at your option.
Contribution
Unless you explicitly state otherwise, any contribution intentionally submitted for inclusion in the work by you, as defined in the Apache-2.0 license, shall be dual licensed as above, without any additional terms or conditions.
Version log
-
0.1.0 : Initial release
-
0.1.1 : Better tags, images in docs point to repository as relative links to images don't seem to work with crates.io
-
0.3 : Better error handling. Replace "anyhow" errors with more useful enum errors (API change). Removed itertools & anyhow dependency.