meta_diff
| Crates.io | meta_diff |
| lib.rs | meta_diff |
| version | 0.0.1 |
| created_at | 2015-06-29 22:43:51.7927+00 |
| updated_at | 2015-12-11 23:54:10.497015+00 |
| description | Autodiff tool for developing scalable Machine Learning algorithms across different platforms with a single source file. |
| homepage | https://github.com/Botev/meta_diff |
| repository | https://github.com/Botev/meta_diff |
| max_upload_size | |
| id | 2494 |
| size | 738,160 |
documentation
README
Meta Diff
Meta Diff is a tool for automatic differentiation and code generation for developing scalable Machine Learning algorithms across different platforms with a single source file. It is implemented in Rust and will be distributed as binaries for different platforms.
[Documentation website] (http://botev.github.io/meta_diff/index.html)
Usage and Installation
When the project is ready it will be distributed as a binary file and will not requrie any form of installation. The usage is from the command line in the format:
diff <source_file>
The command will create a new folder in the current directory with the name of the input file and in it you will find all of the auto generate sources. Note that these might need to be compiled on their own (in the case of C/C++, CUDA or OpenCL) or might directly be used (in the case of Matlab or Python).
The source language
The source file follows a subset of Matlab syntax, but has several important differences. Consider the simple source file below for a feed forward network:
function [L] = mat(@w1,@w2,x,y)
h = tanh(w1 dot vertcat(x,1));
h = tanh(w2 dot vertcat(h,1));
L = l2(h-y,0);
end
The first line defines a funciton mat with four arguments - the first two are parameters and the second two are constatns, which means no gradients will be taken with respect to them. All of the standard operation are considered to be an elementwise operation. Thus the operator * is the so called Hadammart product. The multiplications in the Linear Algebra sense is implemented via the keyword dot. Thus, this snippet calclulates a forward pass over a network, by adding a bias term to each layer using vertcat. The last line specify that we are taking an L2 squared norm of h-y. The second argument to the function specifies along which dimension and 0 has the meaning of all dimensions. When parsing the tool will automatically take a gradient operation, thus for the example this results in the following computation graph (picutre generated by the graphviz module):
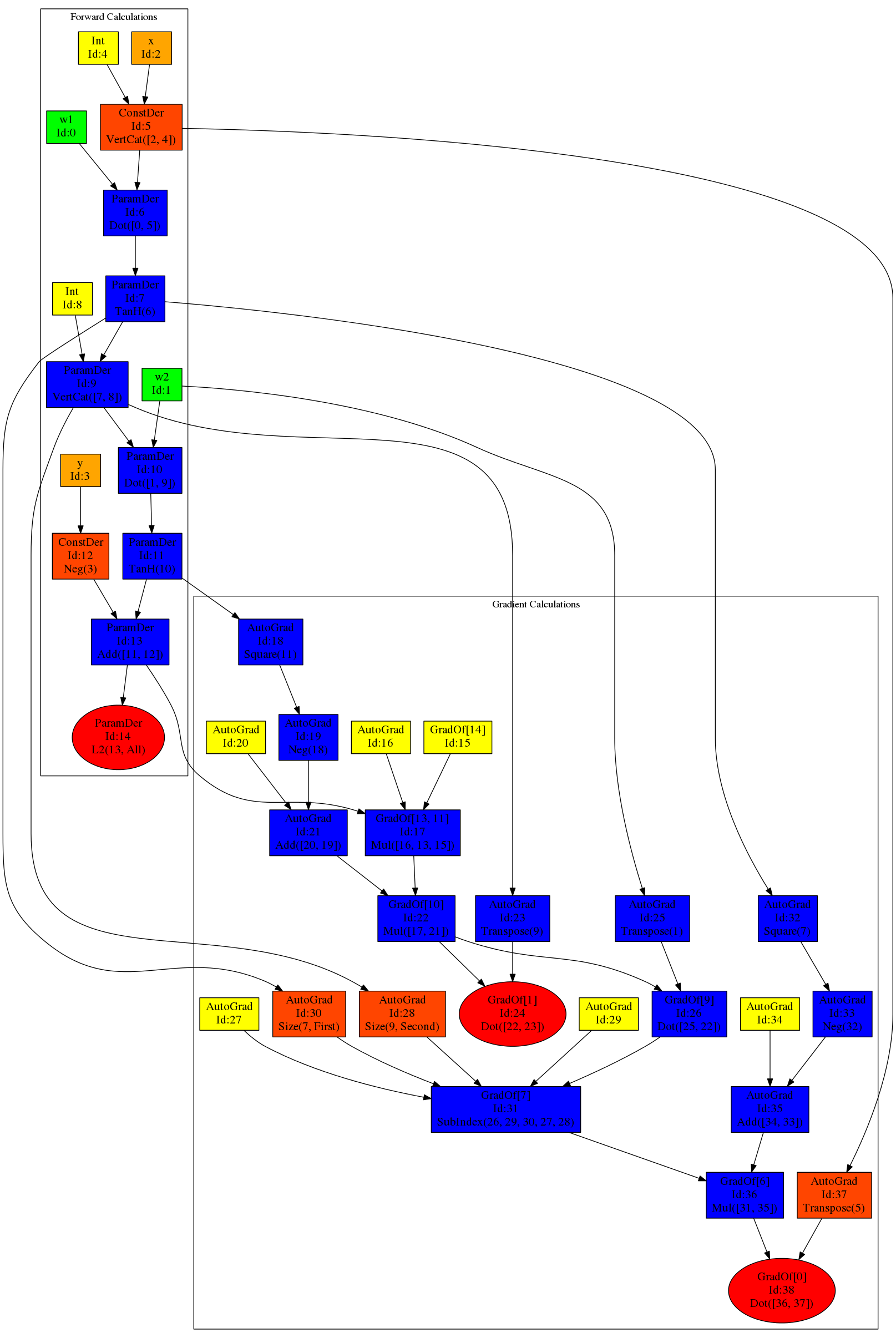
Current stage of development
At the moment the core building blocks of the project have been implemented - the ComputeGraph and the parser.
Currently there are several very important parts which are being implemented:
- Optimisation over the structure of the computation gprah
- Pruning - remove any nodes, which are irrelevant to the output
- Removing redundacies - exhcange nodes which preform the same computation with a single node
- Inverse manipulation - functions which perform an invertion to be replaced by original node - e.g.
log(exp(x))converted tox - Constants folding - combine constatns present in the same operation
- Negation and Division reordering - e.g. convert
-(b + c) + dto(-b) + (-c) + d - Collect n-ary oeprators - e.g. convert
(a+b) + (c+d)toa + b + c + d - Logarithm of a multiplication operator to be exchanged by a sum of lograithm operators
- Product of exponential operators to be exchanged by an exponential of the sum
- Sub indexing optimisation
- Matlab and Eigen code generators
Future goals
There are troumendous amount of possible extensions that can be done in time, but currently what is considered to be the most crucial are:
- Consideration of array support, or some form of map reduce functionality
- For loops and sub routines importing
- OpenCL or CUDA code generation
- Hessian-vector product
Please for any suggestions open an Issue on the issues tracker. Also if you happen to implement some interesting examples please notify us to add them to the example folder!
