quaternion-core
| Crates.io | quaternion-core |
| lib.rs | quaternion-core |
| version | 0.6.1 |
| created_at | 2022-05-07 02:24:09.366474+00 |
| updated_at | 2025-12-14 12:01:25.370451+00 |
| description | Provides quaternion operations and interconversion with several attitude representations. |
| homepage | https://github.com/HamaguRe/quaternion-core.git |
| repository | https://github.com/HamaguRe/quaternion-core.git |
| max_upload_size | |
| id | 581936 |
| size | 121,196 |
documentation
README
quaternion-core
Quaternion library written in Rust.
This crate provides Quaternion operations and interconversion with several rotation
representations as generic functions (supports f32 & f64).
Additionally, it also works in a no_std environment!
Usage
Add this to your Cargo.toml:
[dependencies]
quaternion-core = "0.6"
For use in a no_std environment:
[dependencies.quaternion-core]
version = "0.6"
default-features = false
features = ["libm"]
Conversion
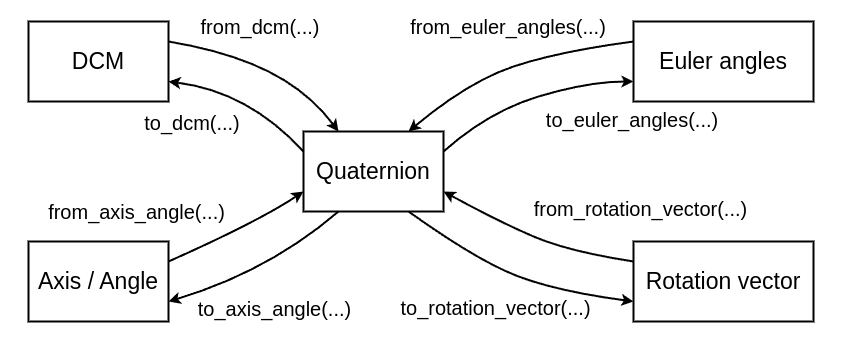
This crate provides functions to convert between quaternions and several rotation representations (as shown in the image above).
In particular, for Euler angles, it is possible to interconversion with 24 different
euler angles (12 each of Intrinsic and Extrinsic) is possible!!
Features
libm
If you set default-features=false (do not import std), you must enable this feature.
In this case, mathematical functions (e.g. sin, cos, sqrt ...) are provided by
libm crate.
fma
When this feature is enabled, the
mul_add
method will be used internally as much as possible.
That is, (s * a) + b will be expanded as s.mul_add(a, b) at compile time.
This crate uses the mul_add method mainly to improve calculation speed, but if the CPU does
not support the FMA (Fused Multiply-Add) instruction or if the libm feature is
enabled, then the calculation is performed by the software implementation.
In this case, it may be rather slower than if the fma feature is not enabled.
norm-sqrt
When this feature is enabled, the default norm(a) implementation is compiled with
dot(a, a).sqrt() instead.
By default, the norm(a) function is implemented in such a way that overflow and
underflow are less likely to occur than with dot(a, a).sqrt(). However, if extremely
large values are not input and underflow is not that much of a concern,
dot(a, a).sqrt() is sufficient (and dot(a, a).sqrt() is faster than the default implementation in most cases).
serde-serialize
When this feature is enabled, RotationSequence and RotationType will both
implement serde::Serialize and serde::Deserialize.
Example
use quaternion_core as quat;
const PI: f64 = std::f64::consts::PI;
const EPSILON: f64 = 1e-12;
fn main() {
// Generates a quaternion representing the
// rotation of π/2[rad] around the y-axis.
let q = quat::from_axis_angle([0.0, 1.0, 0.0], PI/2.0);
// Rotate the point.
let r = quat::point_rotation(q, [2.0, 2.0, 0.0]);
// Check if the calculation is correct.
let diff = quat::sub([0.0, 2.0, -2.0], r);
for val in diff {
assert!( val.abs() < EPSILON );
}
}
Development concept
In creating this crate, I tried to keep the implementation simple and practical.
All functions are implemented in such a way that the computational cost is as small as possible (but not too complex to implement), which is a great advantage for everyone.
Also, since I started creating this crate to experiment with attitude estimation, many parts
were implemented with the intention of running on a microcontroller (e.g. the norm-sqrt feature).
Releases
Release notes are available in RELEASES.md.
License
Licensed under either of Apache License, Version 2.0 or MIT License at your option.
Contribution
Unless you explicitly state otherwise, any contribution intentionally submitted for inclusion in the work by you, as defined in the Apache-2.0 license, shall be dual licensed as above, without any additional terms or conditions.



