rings-snark
| Crates.io | rings-snark |
| lib.rs | rings-snark |
| version | 0.7.0 |
| created_at | 2024-03-28 09:59:18.264792+00 |
| updated_at | 2024-04-30 10:37:07.044702+00 |
| description | IVC SNARK implementation of Rings Network |
| homepage | |
| repository | https://github.com/RingsNetwork/rings-node |
| max_upload_size | |
| id | 1188909 |
| size | 9,180,893 |
documentation
README

Rings SNARK
======================
This crate contains the implementation of Rings SNARK, which is based on Nova
TL;DR
Rings SNARK is a SNARK proof system based on NOVA. It automates the process of transferring circuits written in circom language to the bellpepper proof system used by Rings SNARK. Additionally, it leverages Nova for folding operations. This is beneficial for breaking down large zkSNARK computations and enabling parallel processing.
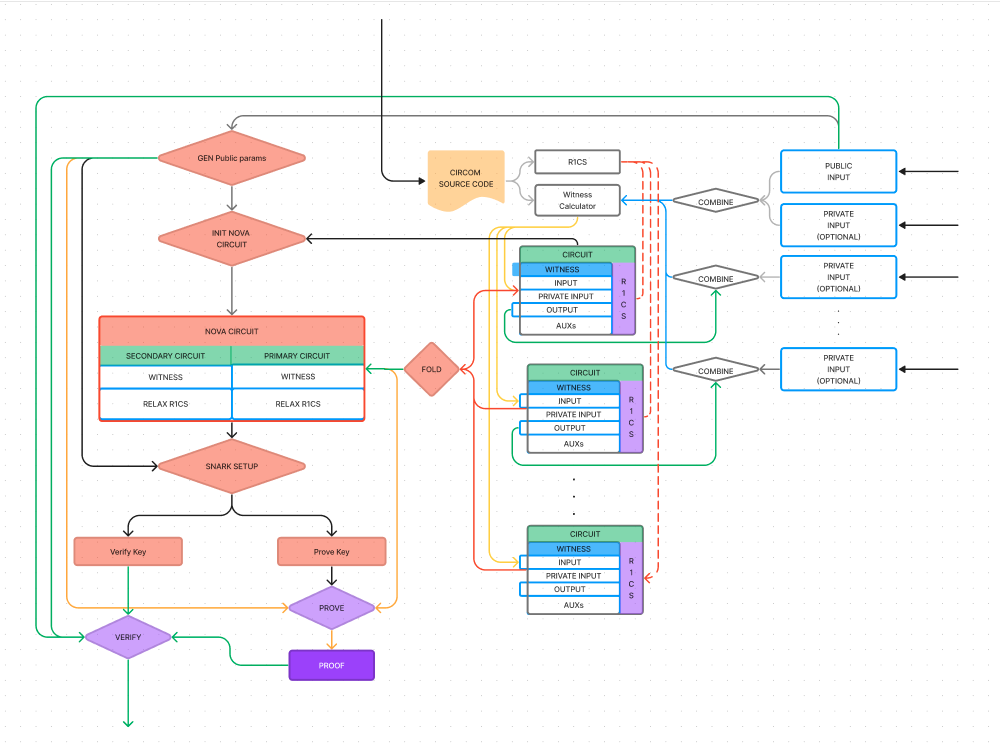
Workflow
The following diagram illustrates the core logic of Rings SNARK. The top side represents the input from circom, including the compiled r1cs and wasm. The right side shows the circuit's input, including public and private input.
WASM Reader
Rings SNARK includes a loader module for Circom Witness Calculator (Wasm). It uses wasmer for reading wasm and transforms it into a Circuit compatible with Nova standards.
RICS Loader
Rings SNARK can read r1cs generated by circom and convert them to the bell pepper proof system. This is based on the work of Circom-Scotia and further adds support for browsers.
Nova Folder
Through Nova, Rings SNARK performs folding computations on circuits. A set of recursive circuits can be folded into two Relax R1CS-based circuits. This allows Rings SNARK to arbitrarily split the circuit list and distribute it across nodes via the Rings Network.
Recursive SNARK
Rings SNARK supports most recursive circuits. It requires that the number of inputs and outputs in a circuit be equal. The output from one step becomes the input for the next, thus creating a recursive process. For circuits not originally designed for recursive SNARK, simple modifications may be necessary. For instance, auxiliary variables can be used to make inputs and outputs recursive, or internal loops can be rewritten as recursive structures. For more details, refer to the merkle tree example in the examples section.

