tritet
| Crates.io | tritet |
| lib.rs | tritet |
| version | 3.0.2 |
| created_at | 2022-06-16 06:40:35.743895+00 |
| updated_at | 2025-12-20 23:19:39.30196+00 |
| description | Triangle and tetrahedron mesh generators |
| homepage | https://github.com/cpmech/tritet |
| repository | https://github.com/cpmech/tritet |
| max_upload_size | |
| id | 607268 |
| size | 3,731,677 |
documentation
README
Triangle and tetrahedron mesh generators
Contents
- Introduction
- Installation
- Setting Cargo.toml
- Examples
- Definitions for Triangle (By J. R. Shewchuk)
- For developers
Introduction
This crate implements Triangle mesh generators by wrapping Triangle
Here, all the data structures accessed by the C/C++ codes are allocated on the "C-side" by (carefully) using "malloc/new." Valgrind is employed to make sure that there are no leaks (hopefully). It should be no performance loss of the C-code.
The code works in multithreaded applications---not exhaustively verified but tested. See, for example, the tests in mem_check_triangle_build.rs and mem_check_tetgen_build.rs
Optional tetrahedron mesh generation is provided by wrapping Tetgen. Tetgen must be enabled via the feature with_tetgen to use the corresponding functionality. In this case, the license of the project becomes AGPL (https://www.gnu.org/licenses/agpl-3.0.html).
See the documentation for further information:
- Tritet documentation - Contains the API reference and examples
License
This project is dual licensed. Without Tetgen, it is licensed under the MIT License. With Tetgen enabled, it is licensed under the AGPL License.
Installation
Install some libraries:
sudo apt install build-essential
Setting Cargo.toml
👆 Check the crate version and update your Cargo.toml accordingly:
[dependencies]
tritet = "*"
Features (for Tetgen)
Use the feature with_tetgen to enable Tetgen functionality. For running tests:
cargo test --features with_tetgen
Examples
Note: set SAVE_FIGURE to true to generate the figures.
Mesh generation using JSON input files
Tritet contains two executables to generate meshes:
trigen2mshto generate quality triangle meshes with boundary markers and volume and angle constraintstetgen2mshto generate quality tetrahedral meshes with boundary markers and volume and angle constraints
Below is a JSON input for trigen2msh:
{
"points": [
[0, 0.0, 0.0],
[0, 1.0, 0.0],
[0, 1.0, 1.0],
[0, 0.0, 1.0],
[0, 0.2, 0.2],
[0, 0.8, 0.2],
[0, 0.8, 0.8],
[0, 0.2, 0.8],
[0, 0.0, 0.5],
[0, 0.2, 0.5],
[0, 0.8, 0.5],
[0, 1.0, 0.5]
],
"segments": [
[-1, 0, 1],
[-1, 1, 2],
[-1, 2, 3],
[-1, 3, 0],
[-1, 4, 5],
[-1, 5, 6],
[-1, 6, 7],
[-1, 7, 4],
[-1, 8, 9],
[-1, 10, 11]
],
"holes": [
[0.5, 0.5]
],
"regions": [
[1, 0.1, 0.1, null],
[2, 0.1, 0.9, null]
]
}
Which can be used as follows:
cargo run --bin trigen2msh -- data/input/example_tri_input.json /tmp/tritet -s -v0.01
Where -s indicates SVG file generation (if Python/Matplotlib is available; otherwise an error arises),
and v0.01 indicates an area (volume) constraint of 0.01. The output is shown below:
Below is a JSON input for tetgen2msh:
{
"points": [
[0, 0.0, 1.0, 0.0],
[0, 0.0, 0.0, 0.0],
[0, 1.0, 1.0, 0.0],
[0, 0.0, 1.0, 1.0]
],
"facets": [
[0, [0, 2, 1]],
[0, [0, 1, 3]],
[0, [0, 3, 2]],
[0, [1, 2, 3]]
],
"holes": [],
"regions": [
[1, 0.1, 0.9, 0.1, null]
]
}
Which can be used as follows:
cargo run --bin tetgen2msh --features with_tetgen -- data/input/example_tet_input.json /tmp/tritet -s -v0.1
Where -s indicates SVG file generation (if Python/Matplotlib is available; otherwise an error arises),
and v0.1 indicates an volume constraint of 0.1. The output is shown below:
2D Delaunay triangulation
use plotpy::Plot;
use tritet::{StrError, Trigen};
const SAVE_FIGURE: bool = false;
fn main() -> Result<(), StrError> {
// allocate data for 10 points
let mut trigen = Trigen::new(10, None, None, None)?;
// set points
trigen
.set_point(0, 0, 0.478554, 0.00869692)?
.set_point(1, 0, 0.13928, 0.180603)?
.set_point(2, 0, 0.578587, 0.760349)?
.set_point(3, 0, 0.903726, 0.975904)?
.set_point(4, 0, 0.0980015, 0.981755)?
.set_point(5, 0, 0.133721, 0.348832)?
.set_point(6, 0, 0.648071, 0.369534)?
.set_point(7, 0, 0.230951, 0.558482)?
.set_point(8, 0, 0.0307942, 0.459123)?
.set_point(9, 0, 0.540745, 0.331184)?;
// generate Delaunay triangulation
trigen.generate_delaunay(false)?;
// draw triangles
if SAVE_FIGURE {
let mut plot = Plot::new();
trigen.draw_triangles(&mut plot, true, true, true, true, None, None, None);
plot.set_equal_axes(true)
.set_figure_size_points(600.0, 600.0)
.save("/tmp/tritet/doc_triangle_delaunay_1.svg")?;
}
Ok(())
}
2D Voronoi tessellation
use plotpy::Plot;
use tritet::{StrError, Trigen};
const SAVE_FIGURE: bool = false;
fn main() -> Result<(), StrError> {
// allocate data for 10 points
let mut trigen = Trigen::new(10, None, None, None)?;
// set points
trigen
.set_point(0, 0, 0.478554, 0.00869692)?
.set_point(1, 0, 0.13928, 0.180603)?
.set_point(2, 0, 0.578587, 0.760349)?
.set_point(3, 0, 0.903726, 0.975904)?
.set_point(4, 0, 0.0980015, 0.981755)?
.set_point(5, 0, 0.133721, 0.348832)?
.set_point(6, 0, 0.648071, 0.369534)?
.set_point(7, 0, 0.230951, 0.558482)?
.set_point(8, 0, 0.0307942, 0.459123)?
.set_point(9, 0, 0.540745, 0.331184)?;
// generate Voronoi tessellation
trigen.generate_voronoi(false)?;
// draw Voronoi diagram
if SAVE_FIGURE {
let mut plot = Plot::new();
trigen.draw_voronoi(&mut plot);
plot.set_equal_axes(true)
.set_figure_size_points(600.0, 600.0)
.save("/tmp/tritet/doc_triangle_voronoi_1.svg")?;
}
Ok(())
}
2D mesh generation using input data structure
use plotpy::Plot;
use tritet::{InputDataTriMesh, StrError, Trigen};
const SAVE_FIGURE: bool = false;
fn main() -> Result<(), StrError> {
// set input data
let input_data = InputDataTriMesh {
points: vec![
(0, 0.0, 0.0), // boundary marker, x, y
(0, 1.0, 0.0),
(0, 1.0, 1.0),
(0, 0.0, 1.0),
(0, 0.2, 0.2),
(0, 0.8, 0.2),
(0, 0.8, 0.8),
(0, 0.2, 0.8),
(0, 0.0, 0.5),
(0, 0.2, 0.5),
(0, 0.8, 0.5),
(0, 1.0, 0.5),
],
segments: vec![
(-1, 0, 1), // boundary marker, point indices
(-1, 1, 2),
(-1, 2, 3),
(-1, 3, 0),
(-1, 4, 5),
(-1, 5, 6),
(-1, 6, 7),
(-1, 7, 4),
(-1, 8, 9),
(-1, 10, 11),
],
holes: vec![
(0.5, 0.5), // x, y
],
regions: vec![
(1, 0.1, 0.1, None), // marker, x, y, max area
(2, 0.1, 0.9, None),
],
};
// allocate generator from input data
let trigen = Trigen::from_input_data(&input_data)?;
// generate o2 mesh without constraints
trigen.generate_mesh(false, true, false, None, None)?;
assert_eq!(trigen.out_ncell(), 12);
// draw mesh
if SAVE_FIGURE {
let mut plot = Plot::new();
trigen.draw_triangles(&mut plot, true, true, true, true, None, None, None);
plot.set_equal_axes(true)
.set_figure_size_points(600.0, 600.0)
.save("/tmp/tritet/doc_triangle_mesh_1.svg")?;
}
Ok(())
}
2D mesh generation using setup functions
use plotpy::Plot;
use tritet::{StrError, Trigen};
const SAVE_FIGURE: bool = false;
fn main() -> Result<(), StrError> {
// allocate data for 12 points, 10 segments, 2 regions, and 1 hole
let mut trigen = Trigen::new(12, Some(10), Some(2), Some(1))?;
// set points
trigen
.set_point(0, 0, 0.0, 0.0)?
.set_point(1, 0, 1.0, 0.0)?
.set_point(2, 0, 1.0, 1.0)?
.set_point(3, 0, 0.0, 1.0)?
.set_point(4, 0, 0.2, 0.2)?
.set_point(5, 0, 0.8, 0.2)?
.set_point(6, 0, 0.8, 0.8)?
.set_point(7, 0, 0.2, 0.8)?
.set_point(8, 0, 0.0, 0.5)?
.set_point(9, 0, 0.2, 0.5)?
.set_point(10, 0, 0.8, 0.5)?
.set_point(11, 0, 1.0, 0.5)?;
// set segments
trigen
.set_segment(0, -1, 0, 1)?
.set_segment(1, -1, 1, 2)?
.set_segment(2, -1, 2, 3)?
.set_segment(3, -1, 3, 0)?
.set_segment(4, -1, 4, 5)?
.set_segment(5, -1, 5, 6)?
.set_segment(6, -1, 6, 7)?
.set_segment(7, -1, 7, 4)?
.set_segment(8, -1, 8, 9)?
.set_segment(9, -1, 10, 11)?;
// set regions
trigen
.set_region(0, 1, 0.1, 0.1, None)?
.set_region(1, 2, 0.1, 0.9, None)?;
// set holes
trigen.set_hole(0, 0.5, 0.5)?;
// generate o2 mesh without constraints
trigen.generate_mesh(false, true, false, None, None)?;
// draw mesh
if SAVE_FIGURE {
let mut plot = Plot::new();
trigen.draw_triangles(&mut plot, true, true, true, true, None, None, None);
plot.set_equal_axes(true)
.set_figure_size_points(600.0, 600.0)
.save("/tmp/tritet/doc_triangle_mesh_1.svg")?;
}
Ok(())
}
3D Delaunay triangulation
Note: Tetgen must be enabled via the feature with_tetgen to run this example.
use plotpy::Plot;
use tritet::{StrError, Tetgen};
const SAVE_FIGURE: bool = false;
fn main() -> Result<(), StrError> {
// allocate data for 8 points
let mut tetgen = Tetgen::new(8, None, None, None)?;
// set points
tetgen
.set_point(0, 0, 0.0, 0.0, 0.0)?
.set_point(1, 0, 1.0, 0.0, 0.0)?
.set_point(2, 0, 1.0, 1.0, 0.0)?
.set_point(3, 0, 0.0, 1.0, 0.0)?
.set_point(4, 0, 0.0, 0.0, 1.0)?
.set_point(5, 0, 1.0, 0.0, 1.0)?
.set_point(6, 0, 1.0, 1.0, 1.0)?
.set_point(7, 0, 0.0, 1.0, 1.0)?;
// generate Delaunay triangulation
tetgen.generate_delaunay(false)?;
// draw edges of tetrahedra
if SAVE_FIGURE {
let mut plot = Plot::new();
tetgen.draw_wireframe(&mut plot, true, true, true, true, None, None, None);
plot.set_equal_axes(true)
.set_figure_size_points(600.0, 600.0)
.save("/tmp/tritet/example_tetgen_delaunay_1.svg")?;
}
Ok(())
}
3D mesh generation using the input data structure
Note: Tetgen must be enabled via the feature with_tetgen to run this example.
use plotpy::Plot;
use tritet::{InputDataTetMesh, StrError, Tetgen};
const SAVE_FIGURE: bool = false;
fn main() -> Result<(), StrError> {
// set input data
let input_data = InputDataTetMesh {
points: vec![
(0, 0.0, 1.0, 0.0), // marker, x, y, z
(0, 0.0, 0.0, 0.0),
(0, 1.0, 1.0, 0.0),
(0, 0.0, 1.0, 1.0),
],
facets: vec![
(0, vec![0, 2, 1]), // marker, point indices
(0, vec![0, 1, 3]),
(0, vec![0, 3, 2]),
(0, vec![1, 2, 3]),
],
holes: vec![], // no holes
regions: vec![(1, 0.1, 0.9, 0.1, None)], // region marker, x, y, z, max volume
};
// allocate generator from input data
let tetgen = Tetgen::from_input_data(&input_data)?;
// generate mesh
let global_max_volume = Some(0.5);
tetgen.generate_mesh(false, false, global_max_volume, None)?;
// draw edges of tetrahedra
if SAVE_FIGURE {
let mut plot = Plot::new();
tetgen.draw_wireframe(&mut plot, true, true, true, true, None, None, None);
plot.set_equal_axes(true)
.set_figure_size_points(600.0, 600.0)
.save("/tmp/tritet/doc_tetgen_mesh_2.svg")?;
}
assert_eq!(tetgen.out_ncell(), 7);
assert_eq!(tetgen.out_npoint(), 10);
Ok(())
}
3D mesh generation using setup functions
Note: Tetgen must be enabled via the feature with_tetgen to run this example.
Note: set SAVE_VTU_FILE to true to generate Paraview file.
use plotpy::Plot;
use tritet::{StrError, Tetgen};
const SAVE_VTU_FILE: bool = false;
const SAVE_FIGURE: bool = false;
fn main() -> Result<(), StrError> {
// allocate data for 16 points and 12 facets
// (one cube/hole inside another cube)
let mut tetgen = Tetgen::new(
16,
Some(vec![
4, 4, 4, 4, 4, 4, // inner cube
4, 4, 4, 4, 4, 4, // outer cube
]),
Some(1),
Some(1),
)?;
// inner cube
tetgen
.set_point(0, 0, 0.0, 0.0, 0.0)?
.set_point(1, 0, 1.0, 0.0, 0.0)?
.set_point(2, 0, 1.0, 1.0, 0.0)?
.set_point(3, 0, 0.0, 1.0, 0.0)?
.set_point(4, 0, 0.0, 0.0, 1.0)?
.set_point(5, 0, 1.0, 0.0, 1.0)?
.set_point(6, 0, 1.0, 1.0, 1.0)?
.set_point(7, 0, 0.0, 1.0, 1.0)?;
// outer cube
tetgen
.set_point(8, 0, -1.0, -1.0, -1.0)?
.set_point(9, 0, 2.0, -1.0, -1.0)?
.set_point(10, 0, 2.0, 2.0, -1.0)?
.set_point(11, 0, -1.0, 2.0, -1.0)?
.set_point(12, 0, -1.0, -1.0, 2.0)?
.set_point(13, 0, 2.0, -1.0, 2.0)?
.set_point(14, 0, 2.0, 2.0, 2.0)?
.set_point(15, 0, -1.0, 2.0, 2.0)?;
// inner cube
tetgen
.set_facet_point(0, 0, 0)?
.set_facet_point(0, 1, 4)?
.set_facet_point(0, 2, 7)?
.set_facet_point(0, 3, 3)?;
tetgen
.set_facet_point(1, 0, 1)?
.set_facet_point(1, 1, 2)?
.set_facet_point(1, 2, 6)?
.set_facet_point(1, 3, 5)?;
tetgen
.set_facet_point(2, 0, 0)?
.set_facet_point(2, 1, 1)?
.set_facet_point(2, 2, 5)?
.set_facet_point(2, 3, 4)?;
tetgen
.set_facet_point(3, 0, 2)?
.set_facet_point(3, 1, 3)?
.set_facet_point(3, 2, 7)?
.set_facet_point(3, 3, 6)?;
tetgen
.set_facet_point(4, 0, 0)?
.set_facet_point(4, 1, 3)?
.set_facet_point(4, 2, 2)?
.set_facet_point(4, 3, 1)?;
tetgen
.set_facet_point(5, 0, 4)?
.set_facet_point(5, 1, 5)?
.set_facet_point(5, 2, 6)?
.set_facet_point(5, 3, 7)?;
// outer cube
tetgen
.set_facet_point(6, 0, 8 + 0)?
.set_facet_point(6, 1, 8 + 4)?
.set_facet_point(6, 2, 8 + 7)?
.set_facet_point(6, 3, 8 + 3)?;
tetgen
.set_facet_point(7, 0, 8 + 1)?
.set_facet_point(7, 1, 8 + 2)?
.set_facet_point(7, 2, 8 + 6)?
.set_facet_point(7, 3, 8 + 5)?;
tetgen
.set_facet_point(8, 0, 8 + 0)?
.set_facet_point(8, 1, 8 + 1)?
.set_facet_point(8, 2, 8 + 5)?
.set_facet_point(8, 3, 8 + 4)?;
tetgen
.set_facet_point(9, 0, 8 + 2)?
.set_facet_point(9, 1, 8 + 3)?
.set_facet_point(9, 2, 8 + 7)?
.set_facet_point(9, 3, 8 + 6)?;
tetgen
.set_facet_point(10, 0, 8 + 0)?
.set_facet_point(10, 1, 8 + 3)?
.set_facet_point(10, 2, 8 + 2)?
.set_facet_point(10, 3, 8 + 1)?;
tetgen
.set_facet_point(11, 0, 8 + 4)?
.set_facet_point(11, 1, 8 + 5)?
.set_facet_point(11, 2, 8 + 6)?
.set_facet_point(11, 3, 8 + 7)?;
// set region and hole
tetgen.set_region(0, 1, -0.9, -0.9, -0.9, None)?;
tetgen.set_hole(0, 0.5, 0.5, 0.5)?;
// generate mesh
tetgen.generate_mesh(false, false, None, None)?;
// generate file for Paraview
if SAVE_VTU_FILE {
tetgen.write_vtu("/tmp/tritet/example_tetgen_mesh_1.vtu")?;
}
// draw edges of tetrahedra
if SAVE_FIGURE {
let mut plot = Plot::new();
tetgen.draw_wireframe(&mut plot, true, true, true, true, None, None, None);
plot.set_equal_axes(true)
.set_figure_size_points(600.0, 600.0)
.save("/tmp/tritet/example_tetgen_mesh_1.svg")?;
}
Ok(())
}
Definitions for Triangle (By J. R. Shewchuk)
This section is part of the text written by J. R. Shewchuk in Triangle. The figures in this section are also Copyright by J. R. Shewchuk.
A Delaunay triangulation (Figure 1) of a vertex set (Figure 2) is a triangulation of the vertex set with the property that no vertex in the vertex set falls in the interior of the circumcircle (circle that passes through all three vertices) of any triangle in the triangulation.
Figure 1. Delaunay triangulation:
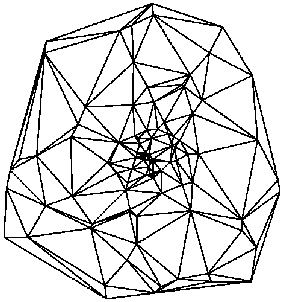
Figure 2. Vertex set (cloud of points):

A Voronoi diagram (Figure 3) of a vertex set is a subdivision of the plane into polygonal regions (some of which may be infinite), where each region is the set of points in the plane that are closer to some input vertex than to any other input vertex. (The Voronoi diagram is the geometric dual of the Delaunay triangulation.)
Figure 3. Voronoi diagram:
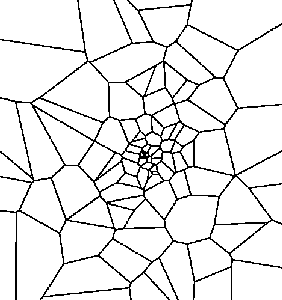
A Planar Straight Line Graph (PSLG, Figure 4) is a collection of vertices and segments. Segments are edges whose endpoints are vertices in the PSLG, and whose presence in any mesh generated from the PSLG is enforced.
Figure 4. Planar Straight Line Graph (PSLG):
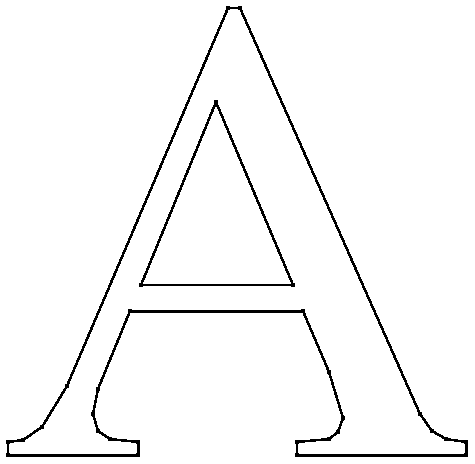
A constrained Delaunay triangulation of a PSLG (Figure 5) is similar to a Delaunay triangulation, but each PSLG segment is present as a single edge in the triangulation. A constrained Delaunay triangulation is not truly a Delaunay triangulation. Some of its triangles might not be Delaunay, but they are all constrained Delaunay.
Figure 5. Constrained Delaunay triangulation of a PSLG:
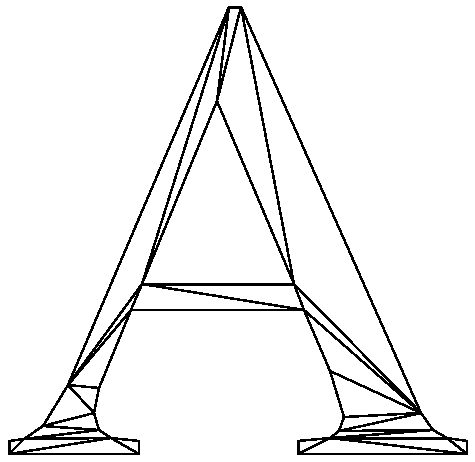
A conforming Delaunay triangulation (CDT, Figure 6) of a PSLG is a true Delaunay triangulation in which each PSLG segment may have been subdivided into several edges by the insertion of additional vertices, called Steiner points. Steiner points are necessary to allow the segments to exist in the mesh while maintaining the Delaunay property. Steiner points are also inserted to meet constraints on the minimum angle and maximum triangle area.
Figure 6. Conforming Delaunay triangulation (CDT):
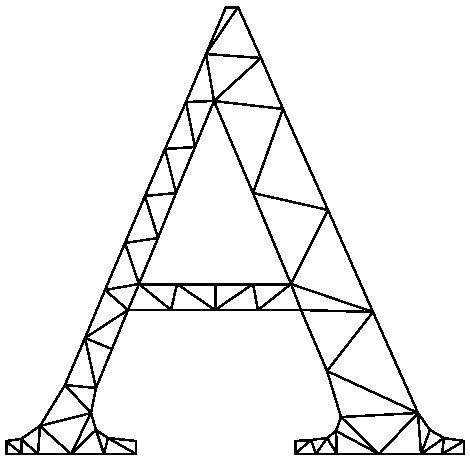
A constrained conforming Delaunay triangulation (CCDT, Figure 7) of a PSLG is a constrained Delaunay triangulation that includes Steiner points. It usually takes fewer vertices to make a good-quality CCDT than a good-quality CDT, because the triangles do not need to be Delaunay (although they still must be constrained Delaunay).
Figure 7. Constrained conforming Delaunay triangulation (CCDT):
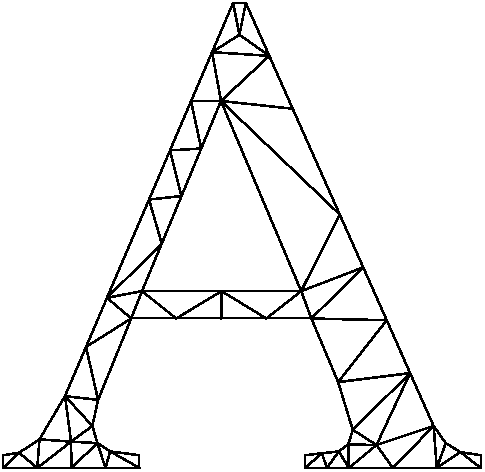
For developers
Install cargo-valgrind:
cargo install cargo-valgrind
Then check for memory leaks (none ;-):
bash memcheck.bash
